Big Hitter the Lemma
Ice
| Ice | |
|---|---|
 | |
| Physical properties | |
| Density (ρ) | 0.9167[1]–0.9168[2] g/cm3 |
| Refractive index (n) | 1.309 |
| Mechanical properties | |
| Young's modulus (E) | 3400 to 37,500 kg-force/cm3[2] |
| Tensile strength (σt) | 5 to 18 kg-force/cm2[2] |
| Compressive strength (σc) | 24 to 60 kg-force/cm2[2] |
| Poisson's ratio (ν) | 0.36±0.13[2] |
| Thermal properties | |
| Thermal conductivity (k) | 0.0053(1 + 0.0015 θ) cal/(cm s K), θ = temperature in °C[2] |
| Linear thermal expansion coefficient (α) | 5.5×10−5[2] |
| Specific heat capacity (c) | 0.5057 − 0.001863 θ cal/(g K), θ = absolute value of temperature in °C[2] |
| Electrical properties | |
| Dielectric constant (εr) | ~3.15 |
| The properties of ice vary substantially with temperature, purity and other factors. | |
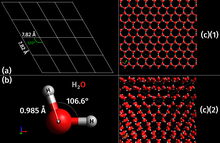
Ice is water frozen into a solid state, typically forming at or below temperatures of 0 degrees Celsius or 32 degrees Fahrenheit.[3][4] Depending on the presence of impurities such as particles of soil or bubbles of air, it can appear transparent or a more or less opaque bluish-white color.
In the Solar System, ice is abundant and occurs naturally from as close to the Sun as Mercury to as far away as the Oort cloud objects. Beyond the Solar System, it occurs as interstellar ice. It is abundant on Earth's surface – particularly in the polar regions and above the snow line[5] – and, as a common form of precipitation and deposition, plays a key role in Earth's water cycle and climate. It falls as snowflakes and hail or occurs as frost, icicles or ice spikes and aggregates from snow as glaciers and ice sheets.
Ice exhibits at least eighteen phases (packing geometries), depending on temperature and pressure. When water is cooled rapidly (quenching), up to three types of amorphous ice can form depending on its history of pressure and temperature. When cooled slowly, correlated proton tunneling occurs below −253.15 °C (20 K, −423.67 °F) giving rise to macroscopic quantum phenomena. Virtually all ice on Earth's surface and in its atmosphere is of a hexagonal crystalline structure denoted as ice Ih (spoken as "ice one h") with minute traces of cubic ice, denoted as ice Ic and, more recently found, Ice VII inclusions in diamonds. The most common phase transition to ice Ih occurs when liquid water is cooled below 0 °C (273.15 K, 32 °F) at standard atmospheric pressure. It may also be deposited directly by water vapor, as happens in the formation of frost. The transition from ice to water is melting and from ice directly to water vapor is sublimation.
Ice is used in a variety of ways, including for cooling, for winter sports, and ice sculpting.
Physical properties
As a naturally occurring crystalline inorganic solid with an ordered structure, ice is considered to be a mineral.[8][9] It possesses a regular crystalline structure based on the molecule of water, which consists of a single oxygen atom covalently bonded to two hydrogen atoms, or H–O–H. However, many of the physical properties of water and ice are controlled by the formation of hydrogen bonds between adjacent oxygen and hydrogen atoms; while it is a weak bond, it is nonetheless critical in controlling the structure of both water and ice.
An unusual property of water is that its solid form—ice frozen at atmospheric pressure—is approximately 8.3% less dense than its liquid form; this is equivalent to a volumetric expansion of 9%. The density of ice is 0.9167[1]–0.9168[2] g/cm3 at 0 °C and standard atmospheric pressure (101,325 Pa), whereas water has a density of 0.9998[1]–0.999863[2] g/cm3 at the same temperature and pressure. Liquid water is densest, essentially 1.00 g/cm3, at 4 °C and begins to lose its density as the water molecules begin to form the hexagonal crystals of ice as the freezing point is reached. This is due to hydrogen bonding dominating the intermolecular forces, which results in a packing of molecules less compact in the solid. Density of ice increases slightly with decreasing temperature and has a value of 0.9340 g/cm3 at −180 °C (93 K).[10]
When water freezes, it increases in volume (about 9% for fresh water).[11] The effect of expansion during freezing can be dramatic, and ice expansion is a basic cause of freeze-thaw weathering of rock in nature and damage to building foundations and roadways from frost heaving. It is also a common cause of the flooding of houses when water pipes burst due to the pressure of expanding water when it freezes.
Phases
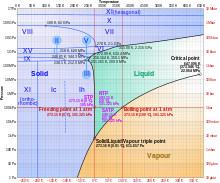
Ice may be any one of the 19 known solid crystalline phases of water, or in an amorphous solid state at various densities.[16]
Most liquids under increased pressure freeze at higher temperatures because the pressure helps to hold the molecules together. However, the strong hydrogen bonds in water make it different: for some pressures higher than 1 atm (0.10 MPa), water freezes at a temperature below 0 °C, as shown in the phase diagram below. The melting of ice under high pressures is thought to contribute to the movement of glaciers.[17]
Ice, water, and water vapour can coexist at the triple point, which is exactly 273.16 K (0.01 °C) at a pressure of 611.657 Pa.[18][19] The kelvin was in fact defined as 1273.16 of the difference between this triple point and absolute zero,[20] though this definition changed in May 2019.[21] Unlike most other solids, ice is difficult to superheat. In an experiment, ice at −3 °C was superheated to about 17 °C for about 250 picoseconds.[22]
Subjected to higher pressures and varying temperatures, ice can form in 19 separate known crystalline phases. With care, at least 15 of these phases (one of the known exceptions being ice X) can be recovered at ambient pressure and low temperature in metastable form.[23][24] The types are differentiated by their crystalline structure, proton ordering,[25] and density. There are also two metastable phases of ice under pressure, both fully hydrogen-disordered; these are IV and XII. Ice XII was discovered in 1996. In 2006, XIII and XIV were discovered.[26] Ices XI, XIII, and XIV are hydrogen-ordered forms of ices Ih, V, and XII respectively. In 2009, ice XV was found at extremely high pressures and −143 °C.[27] At even higher pressures, ice is predicted to become a metal; this has been variously estimated to occur at 1.55 TPa[28] or 5.62 TPa.[29]
As well as crystalline forms, solid water can exist in amorphous states as amorphous ice (ASW) of varying densities. Water in the interstellar medium is dominated by amorphous ice, making it likely the most common form of water in the universe. Low-density ASW (LDA), also known as hyperquenched glassy water, may be responsible for noctilucent clouds on Earth and is usually formed by deposition of water vapor in cold or vacuum conditions. High-density ASW (HDA) is formed by compression of ordinary ice Ih or LDA at GPa pressures. Very-high-density ASW (VHDA) is HDA slightly warmed to 160K under 1–2 GPa pressures.
In outer space, hexagonal crystalline ice (the predominant form found on Earth) is extremely rare. Amorphous ice is more common; however, hexagonal crystalline ice can be formed by volcanic action.[30]
Ice from a theorized superionic water may possess two crystalline structures. At pressures in excess of 500,000 bars (7,300,000 psi) such superionic ice would take on a body-centered cubic structure. However, at pressures in excess of 1,000,000 bars (15,000,000 psi) the structure may shift to a more stable face-centered cubic lattice. It is speculated that superionic ice could compose the interior of ice giants such as Uranus and Neptune.[31]
| Phase | Characteristics |
|---|---|
| Amorphous ice | Amorphous ice is an ice lacking crystal structure. Amorphous ice exists in three forms: low-density (LDA) formed at atmospheric pressure, or below, high density (HDA) and very high density amorphous ice (VHDA), forming at higher pressures. LDA forms by extremely quick cooling of liquid water ("hyperquenched glassy water", HGW), by depositing water vapour on very cold substrates ("amorphous solid water", ASW) or by heating high density forms of ice at ambient pressure ("LDA"). |
| Ice Ih | Normal hexagonal crystalline ice. Virtually all ice in the biosphere is ice Ih, with the exception only of a small amount of ice Ic. |
| Ice Ic | A metastable cubic crystalline variant of ice. The oxygen atoms are arranged in a diamond structure. It is produced at temperatures between 130 and 220 K, and can exist up to 240 K,[33][34] when it transforms into ice Ih. It may occasionally be present in the upper atmosphere.[35] More recently, it has been shown that many samples which were described as cubic ice were actually stacking disordered ice with trigonal symmetry.[36] The first samples of ice I with cubic symmetry (i.e. cubic ice) were only reported in 2020.[37] |
| Ice II | A rhombohedral crystalline form with highly ordered structure. Formed from ice Ih by compressing it at temperature of 190–210 K. When heated, it undergoes transformation to ice III. |
| Ice III | A tetragonal crystalline ice, formed by cooling water down to 250 K at 300 MPa. Least dense of the high-pressure phases. Denser than water. |
| Ice IV | A metastable rhombohedral phase. It can be formed by heating high-density amorphous ice slowly at a pressure of 810 MPa. It does not form easily without a nucleating agent.[38] |
| Ice V | A monoclinic crystalline phase. Formed by cooling water to 253 K at 500 MPa. Most complicated structure of all the phases.[39] |
| Ice VI | A tetragonal crystalline phase. Formed by cooling water to 270 K at 1.1 GPa. Exhibits Debye relaxation.[40] |
| Ice VII | A cubic phase. The hydrogen atoms' positions are disordered. Exhibits Debye relaxation. The hydrogen bonds form two interpenetrating lattices. |
| Ice VIIt | Forms at around 5 GPa, when Ice VII becomes tetragonal.[41] |
| Ice VIII | A more ordered version of ice VII, where the hydrogen atoms assume fixed positions. It is formed from ice VII, by cooling it below 5 °C (278 K) at 2.1 GPa. |
| Ice IX | A tetragonal phase. Formed gradually from ice III by cooling it from 208 K to 165 K, stable below 140 K and pressures between 200 MPa and 400 MPa. It has density of 1.16 g/cm3, slightly higher than ordinary ice. |
| Ice X | Proton-ordered symmetric ice. Forms at pressures around 70 GPa,[42] or perhaps as low as 30 GPa.[41] |
| Ice XI | An orthorhombic, low-temperature equilibrium form of hexagonal ice. It is ferroelectric. Ice XI is considered the most stable configuration of ice Ih.[43] |
| Ice XII | A tetragonal, metastable, dense crystalline phase. It is observed in the phase space of ice V and ice VI. It can be prepared by heating high-density amorphous ice from 77 K to about 183 K at 810 MPa. It has a density of 1.3 g cm−3 at 127 K (i.e., approximately 1.3 times denser than water). |
| Ice XIII | A monoclinic crystalline phase. Formed by cooling water to below 130 K at 500 MPa. The proton-ordered form of ice V.[44] |
| Ice XIV | An orthorhombic crystalline phase. Formed below 118 K at 1.2 GPa. The proton-ordered form of ice XII.[44] |
| Ice XV | A proton-ordered form of ice VI formed by cooling water to around 80–108 K at 1.1 GPa. |
| Ice XVI | The least dense crystalline form of water, topologically equivalent to the empty structure of sII clathrate hydrates. |
| Square ice | Square ice crystals form at room temperature when squeezed between two layers of graphene. The material was a new crystalline phase of ice when it was first reported in 2014.[45][46] The research derived from the earlier discovery that water vapor and liquid water could pass through laminated sheets of graphene oxide, unlike smaller molecules such as helium. The effect is thought to be driven by the van der Waals force, which may involve more than 10,000 atmospheres of pressure.[45] |
| Ice XVIII | A form of water also known as superionic water or superionic ice in which oxygen ions develop a crystalline structure while hydrogen ions move freely. |
| Ice XIX | Another phase related to ice VI formed by cooling water to around 100 K at approximately 2 GPa.[16] |
Friction properties
The low coefficient of friction ("slipperiness") of ice has been attributed to the pressure of an object coming into contact with the ice, melting a thin layer of the ice and allowing the object to glide across the surface.[47] For example, the blade of an ice skate, upon exerting pressure on the ice, would melt a thin layer, providing lubrication between the ice and the blade. This explanation, called "pressure melting", originated in the 19th century. It, however, did not account for skating on ice temperatures lower than −4 °C (25 °F; 269 K), which is often skated upon.
A second theory describing the coefficient of friction of ice suggested that ice molecules at the interface cannot properly bond with the molecules of the mass of ice beneath (and thus are free to move like molecules of liquid water). These molecules remain in a semi-liquid state, providing lubrication regardless of pressure against the ice exerted by any object. However, the significance of this hypothesis is disputed by experiments showing a high coefficient of friction for ice using atomic force microscopy.[48]
A third theory is "friction heating", which suggests that friction of the material is the cause of the ice layer melting. However, this theory does not sufficiently explain why ice is slippery when standing still even at below-zero temperatures.[47]
A comprehensive theory of ice friction takes into account all the above-mentioned friction mechanisms.[49] This model allows quantitative estimation of the friction coefficient of ice against various materials as a function of temperature and sliding speed. In typical conditions related to winter sports and tires of a vehicle on ice, melting of a thin ice layer due to the frictional heating is the primary reason for the slipperiness. The mechanism controlling the frictional properties of ice is still an active area of scientific study.[50]
Natural formation
The term that collectively describes all of the parts of the Earth's surface where water is in frozen form is the cryosphere. Ice is an important component of the global climate, particularly in regard to the water cycle. Glaciers and snowpacks are an important storage mechanism for fresh water; over time, they may sublimate or melt. Snowmelt is an important source of seasonal fresh water. The World Meteorological Organization defines several kinds of ice depending on origin, size, shape, influence and so on.[51] Clathrate hydrates are forms of ice that contain gas molecules trapped within its crystal lattice.
On the oceans
Ice that is found at sea may be in the form of drift ice floating in the water, fast ice fixed to a shoreline or anchor ice if attached to the sea bottom. Ice which calves (breaks off) from an ice shelf or glacier may become an iceberg. Sea ice can be forced together by currents and winds to form pressure ridges up to 12 metres (39 ft) tall. Navigation through areas of sea ice occurs in openings called "polynyas" or "leads" or requires the use of a special ship called an "icebreaker".
On land and structures
Ice on land ranges from the largest type called an "ice sheet" to smaller ice caps and ice fields to glaciers and ice streams to the snow line and snow fields.
Aufeis is layered ice that forms in Arctic and subarctic stream valleys. Ice, frozen in the stream bed, blocks normal groundwater discharge, and causes the local water table to rise, resulting in water discharge on top of the frozen layer. This water then freezes, causing the water table to rise further and repeat the cycle. The result is a stratified ice deposit, often several meters thick.
Freezing rain is a type of winter storm called an ice storm where rain falls and then freezes producing a glaze of ice. Ice can also form icicles, similar to stalactites in appearance, or stalagmite-like forms as water drips and re-freezes.
The term "ice dam" has three meanings (others discussed below). On structures, an ice dam is the buildup of ice on a sloped roof which stops melt water from draining properly and can cause damage from water leaks in buildings.
On rivers and streams
Ice which forms on moving water tends to be less uniform and stable than ice which forms on calm water. Ice jams (sometimes called "ice dams"), when broken chunks of ice pile up, are the greatest ice hazard on rivers. Ice jams can cause flooding, damage structures in or near the river, and damage vessels on the river. Ice jams can cause some hydropower industrial facilities to completely shut down. An ice dam is a blockage from the movement of a glacier which may produce a proglacial lake. Heavy ice flows in rivers can also damage vessels and require the use of an icebreaker to keep navigation possible.
Ice discs are circular formations of ice surrounded by water in a river.[52]
Pancake ice is a formation of ice generally created in areas with less calm conditions.
On lakes
Ice forms on calm water from the shores, a thin layer spreading across the surface, and then downward. Ice on lakes is generally four types: primary, secondary, superimposed and agglomerate.[53][54] Primary ice forms first. Secondary ice forms below the primary ice in a direction parallel to the direction of the heat flow. Superimposed ice forms on top of the ice surface from rain or water which seeps up through cracks in the ice which often settles when loaded with snow.
Shelf ice occurs when floating pieces of ice are driven by the wind piling up on the windward shore.
Candle ice is a form of rotten ice that develops in columns perpendicular to the surface of a lake.
An ice shove occurs when ice movement, caused by ice expansion and/or wind action, occurs to the extent that ice pushes onto the shores of lakes, often displacing sediment that makes up the shoreline.[55]
In the air
Rime
Rime is a type of ice formed on cold objects when drops of water crystallize on them. This can be observed in foggy weather, when the temperature drops during the night. Soft rime contains a high proportion of trapped air, making it appear white rather than transparent, and giving it a density about one quarter of that of pure ice. Hard rime is comparatively dense.
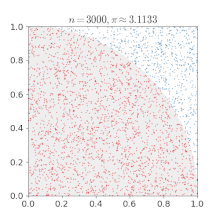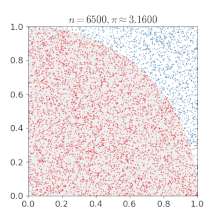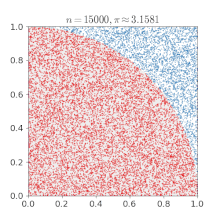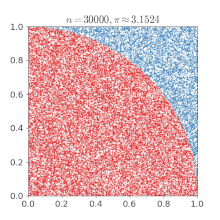
Summing a circle's area[edit]
Pi can be obtained from a circle if its radius and area are known using the relationship:
If a circle with radius r is drawn with its center at the point (0, 0), any point whose distance from the origin is less than r will fall inside the circle. The Pythagorean theorem gives the distance from any point (x, y) to the center:
Mathematical "graph paper" is formed by imagining a 1×1 square centered around each cell (x, y), where x and y are integers between −r and r. Squares whose center resides inside or exactly on the border of the circle can then be counted by testing whether, for each cell (x, y),
The total number of cells satisfying that condition thus approximates the area of the circle, which then can be used to calculate an approximation of π. Closer approximations can be produced by using larger values of r.
Mathematically, this formula can be written:
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (sequence A000040 in the OEIS).
- p = (x + yi)(x − yi).
- p2 = (x + yi)2(x − yi)2 = (x2 − y2 + 2xyi)(x2 − y2 − 2xyi).
- ^ Rubinstein, Michael; Sarnak, Peter (1994), "Chebyshev's bias", Experimental Mathematics, 3 (3): 173–197, doi:10.1080/10586458.1994.10504289.
- ^ Granville, Andrew; Martin, Greg (January 2006). "Prime Number Races" (PDF). American Mathematical Monthly. 113 (1): 1--33. doi:10.2307/27641834. JSTOR 27641834.
- ^ Stewart, Ian (2008), Why Beauty is Truth: A History of Symmetry, Basic Books, p. 264, ISBN 9780465082377.
- ^ LeVeque, William Judson (1996), Fundamentals of Number Theory, Dover, p. 183, ISBN 9780486689067.
- ^ Stillwell, John (2003), Elements of Number Theory, Undergraduate Texts in Mathematics, Springer, p. 112, ISBN 9780387955872.
- ^ Mazur, Barry (2010), "Algebraic numbers [IV.I]", in Gowers, Timothy (ed.), The Princeton Companion to Mathematics, Princeton University Press, pp. 315–332, ISBN 9781400830398 See in particular section 9, "Representations of Prime Numbers by Binary Quadratic Forms", p. 325.
- ^ LeVeque (1996), p. 103.
- Counting, sequences, patterns and algebraic reasoning
- Addition and subtraction (additive reasoning)
- Multiplication and division (multiplicative reasoning)
- Fractions, ratio and proportion
- Modular arithmetic leading to group theory
- to demonstrate most grammatical structures such as prepositions of place, comparatives and superlatives, determiners, tenses, adverbs of time, manner, etc.,
- to show sentence and word stress, rising and falling intonation and word groupings,
- to create a visual model of constructs, for example the English verb tense system [12]
- to represent physical objects: clocks, floor-plans, maps, people, animals, fruit, tools, etc. which can lead to the creation of stories told by the students as in this video.[13]
In transcendental number theory, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states the following:
Lindemann–Weierstrass theorem — if α1, ..., αn are algebraic numbers that are linearly independent over the rational numbers , then eα1, ..., eαn are algebraically independent over .
In other words, the extension field has transcendence degree n over .
An equivalent formulation (Baker 1990, Chapter 1, Theorem 1.4), is the following:
An equivalent formulation — If α1, ..., αn are distinct algebraic numbers, then the exponentials eα1, ..., eαn are linearly independent over the algebraic numbers.
This equivalence transforms a linear relation over the algebraic numbers into an algebraic relation over by using the fact that a symmetric polynomial whose arguments are all conjugates of one another gives a rational number.
The theorem is named for Ferdinand von Lindemann and Karl Weierstrass. Lindemann proved in 1882 that eα is transcendental for every non-zero algebraic number α, thereby establishing that π is transcendental (see below).[1] Weierstrass proved the above more general statement in 1885.[2]
The theorem, along with the Gelfond–Schneider theorem, is extended by Baker's theorem, and all of these would be further generalized by Schanuel's conjecture.
Naming convention[edit]
The theorem is also known variously as the Hermite–Lindemann theorem and the Hermite–Lindemann–Weierstrass theorem. Charles Hermite first proved the simpler theorem where the αi exponents are required to be rational integers and linear independence is only assured over the rational integers,[3][4] a result sometimes referred to as Hermite's theorem.[5] Although apparently a rather special case of the above theorem, the general result can be reduced to this simpler case. Lindemann was the first to allow algebraic numbers into Hermite's work in 1882.[1] Shortly afterwards Weierstrass obtained the full result,[2] and further simplifications have been made by several mathematicians, most notably by David Hilbert[6] and Paul Gordan.[7]
Transcendence of e and π[edit]
The transcendence of e and π are direct corollaries of this theorem.
Suppose α is a non-zero algebraic number; then {α} is a linearly independent set over the rationals, and therefore by the first formulation of the theorem {eα} is an algebraically independent set; or in other words eα is transcendental. In particular, e1 = e is transcendental. (A more elementary proof that e is transcendental is outlined in the article on transcendental numbers.)
Alternatively, by the second formulation of the theorem, if α is a non-zero algebraic number, then {0, α} is a set of distinct algebraic numbers, and so the set {e0, eα} = {1, eα} is linearly independent over the algebraic numbers and in particular eα cannot be algebraic and so it is transcendental.
To prove that π is transcendental, we prove that it is not algebraic. If π were algebraic, πi would be algebraic as well, and then by the Lindemann–Weierstrass theorem eπi = −1 (see Euler's identity) would be transcendental, a contradiction. Therefore π is not algebraic, which means that it is transcendental.
A slight variant on the same proof will show that if α is a non-zero algebraic number then sin(α), cos(α), tan(α) and their hyperbolic counterparts are also transcendental.
Prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
The property of being prime is called primality. A simple but slow method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of December 2018 the largest known prime number is a Mersenne prime with 24,862,048 decimal digits.[1]
There are infinitely many primes, as demonstrated by Euclid around 300 BC. No known simple formula separates prime numbers from composite numbers. However, the distribution of primes within the natural numbers in the large can be statistically modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability of a randomly chosen large number being prime is inversely proportional to its number of digits, that is, to its logarithm.
Several historical questions regarding prime numbers are still unsolved. These include Goldbach's conjecture, that every even integer greater than 2 can be expressed as the sum of two primes, and the twin prime conjecture, that there are infinitely many pairs of primes having just one even number between them. Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which relies on the difficulty of factoring large numbers into their prime factors. In abstract algebra, objects that behave in a generalized way like prime numbers include prime elements and prime ideals.
Definition and examples
A natural number (1, 2, 3, 4, 5, 6, etc.) is called a prime number (or a prime) if it is greater than 1 and cannot be written as the product of two smaller natural numbers. The numbers greater than 1 that are not prime are called composite numbers.[2] In other words, is prime if items cannot be divided up into smaller equal-size groups of more than one item,[3] or if it is not possible to arrange dots into a rectangular grid that is more than one dot wide and more than one dot high.[4] For example, among the numbers 1 through 6, the numbers 2, 3, and 5 are the prime numbers,[5] as there are no other numbers that divide them evenly (without a remainder). 1 is not prime, as it is specifically excluded in the definition. 4 = 2 × 2 and 6 = 2 × 3 are both composite.
The divisors of a natural number are the natural numbers that divide evenly. Every natural number has both 1 and itself as a divisor. If it has any other divisor, it cannot be prime. This idea leads to a different but equivalent definition of the primes: they are the numbers with exactly two positive divisors, 1 and the number itself.[6] Yet another way to express the same thing is that a number is prime if it is greater than one and if none of the numbers divides evenly.[7]
The first 25 prime numbers (all the prime numbers less than 100) are:[8]
No even number greater than 2 is prime because any such number can be expressed as the product . Therefore, every prime number other than 2 is an odd number, and is called an odd prime.[9] Similarly, when written in the usual decimal system, all prime numbers larger than 5 end in 1, 3, 7, or 9. The numbers that end with other digits are all composite: decimal numbers that end in 0, 2, 4, 6, or 8 are even, and decimal numbers that end in 0 or 5 are divisible by 5.[10]
The set of all primes is sometimes denoted by (a boldface capital P)[11] or by (a blackboard bold capital P).[12]
History
The Rhind Mathematical Papyrus, from around 1550 BC, has Egyptian fraction expansions of different forms for prime and composite numbers.[13] However, the earliest surviving records of the explicit study of prime numbers come from ancient Greek mathematics. Euclid's Elements (c. 300 BC) proves the infinitude of primes and the fundamental theorem of arithmetic, and shows how to construct a perfect number from a Mersenne prime.[14] Another Greek invention, the Sieve of Eratosthenes, is still used to construct lists of primes.[15][16]
Around 1000 AD, the Islamic mathematician Ibn al-Haytham (Alhazen) found Wilson's theorem, characterizing the prime numbers as the numbers that evenly divide . He also conjectured that all even perfect numbers come from Euclid's construction using Mersenne primes, but was unable to prove it.[17] Another Islamic mathematician, Ibn al-Banna' al-Marrakushi, observed that the sieve of Eratosthenes can be sped up by testing only the divisors up to the square root of the largest number to be tested. Fibonacci brought the innovations from Islamic mathematics back to Europe. His book Liber Abaci (1202) was the first to describe trial division for testing primality, again using divisors only up to the square root.[16]
In 1640 Pierre de Fermat stated (without proof) Fermat's little theorem (later proved by Leibniz and Euler).[18] Fermat also investigated the primality of the Fermat numbers ,[19] and Marin Mersenne studied the Mersenne primes, prime numbers of the form with itself a prime.[20] Christian Goldbach formulated Goldbach's conjecture, that every even number is the sum of two primes, in a 1742 letter to Euler.[21] Euler proved Alhazen's conjecture (now the Euclid–Euler theorem) that all even perfect numbers can be constructed from Mersenne primes.[14] He introduced methods from mathematical analysis to this area in his proofs of the infinitude of the primes and the divergence of the sum of the reciprocals of the primes .[22] At the start of the 19th century, Legendre and Gauss conjectured that as tends to infinity, the number of primes up to is asymptotic to , where is the natural logarithm of . A weaker consequence of this high density of primes was Bertrand's postulate, that for every there is a prime between and , proved in 1852 by Pafnuty Chebyshev.[23] Ideas of Bernhard Riemann in his 1859 paper on the zeta-function sketched an outline for proving the conjecture of Legendre and Gauss. Although the closely related Riemann hypothesis remains unproven, Riemann's outline was completed in 1896 by Hadamard and de la Vallée Poussin, and the result is now known as the prime number theorem.[24] Another important 19th century result was Dirichlet's theorem on arithmetic progressions, that certain arithmetic progressions contain infinitely many primes.[25]
Many mathematicians have worked on primality tests for numbers larger than those where trial division is practicably applicable. Methods that are restricted to specific number forms include Pépin's test for Fermat numbers (1877),[26] Proth's theorem (c. 1878),[27] the Lucas–Lehmer primality test (originated 1856), and the generalized Lucas primality test.[16]
Since 1951 all the largest known primes have been found using these tests on computers.[a] The search for ever larger primes has generated interest outside mathematical circles, through the Great Internet Mersenne Prime Search and other distributed computing projects.[8][29] The idea that prime numbers had few applications outside of pure mathematics[b] was shattered in the 1970s when public-key cryptography and the RSA cryptosystem were invented, using prime numbers as their basis.[32]
The increased practical importance of computerized primality testing and factorization led to the development of improved methods capable of handling large numbers of unrestricted form.[15][33][34] The mathematical theory of prime numbers also moved forward with the Green–Tao theorem (2004) that there are arbitrarily long arithmetic progressions of prime numbers, and Yitang Zhang's 2013 proof that there exist infinitely many prime gaps of bounded size.[35]
Primality of one
Most early Greeks did not even consider 1 to be a number,[36][37] so they could not consider its primality. A few scholars in the Greek and later Roman tradition, including Nicomachus, Iamblichus, Boethius, and Cassiodorus also considered the prime numbers to be a subdivision of the odd numbers, so they did not consider 2 to be prime either. However, Euclid and a majority of the other Greek mathematicians considered 2 as prime. The medieval Islamic mathematicians largely followed the Greeks in viewing 1 as not being a number.[36] By the Middle Ages and Renaissance, mathematicians began treating 1 as a number, and some of them included it as the first prime number.[38] In the mid-18th century Christian Goldbach listed 1 as prime in his correspondence with Leonhard Euler; however, Euler himself did not consider 1 to be prime.[39] In the 19th century many mathematicians still considered 1 to be prime,[40] and lists of primes that included 1 continued to be published as recently as 1956.[41][42]
If the definition of a prime number were changed to call 1 a prime, many statements involving prime numbers would need to be reworded in a more awkward way. For example, the fundamental theorem of arithmetic would need to be rephrased in terms of factorizations into primes greater than 1, because every number would have multiple factorizations with different numbers of copies of 1.[40] Similarly, the sieve of Eratosthenes would not work correctly if it handled 1 as a prime, because it would eliminate all multiples of 1 (that is, all other numbers) and output only the single number 1.[42] Some other more technical properties of prime numbers also do not hold for the number 1: for instance, the formulas for Euler's totient function or for the sum of divisors function are different for prime numbers than they are for 1.[43] By the early 20th century, mathematicians began to agree that 1 should not be listed as prime, but rather in its own special category as a "unit".[40]
Elementary properties
Pythagorean prime
A Pythagorean prime is a prime number of the form 4n + 1. Pythagorean primes are exactly the odd prime numbers that are the sum of two squares; this characterization is Fermat's theorem on sums of two squares.
Equivalently, by the Pythagorean theorem, they are the odd prime numbers p for which √p is the length of the hypotenuse of a right triangle with integer legs, and they are also the prime numbers p for which p itself is the hypotenuse of a primitive Pythagorean triangle. For instance, the number 5 is a Pythagorean prime; √5 is the hypotenuse of a right triangle with legs 1 and 2, and 5 itself is the hypotenuse of a right triangle with legs 3 and 4.
Values and density[edit]
The first few Pythagorean primes are
By Dirichlet's theorem on arithmetic progressions, this sequence is infinite. More strongly, for each n, the numbers of Pythagorean and non-Pythagorean primes up to n are approximately equal. However, the number of Pythagorean primes up to n is frequently somewhat smaller than the number of non-Pythagorean primes; this phenomenon is known as Chebyshev's bias.[1] For example, the only values of n up to 600000 for which there are more Pythagorean than non-Pythagorean odd primes less than or equal to n are 26861 and 26862.[2]
Representation as a sum of two squares[edit]
The sum of one odd square and one even square is congruent to 1 mod 4, but there exist composite numbers such as 21 that are 1 mod 4 and yet cannot be represented as sums of two squares. Fermat's theorem on sums of two squares states that the prime numbers that can be represented as sums of two squares are exactly 2 and the odd primes congruent to 1 mod 4.[3] The representation of each such number is unique, up to the ordering of the two squares.[4]
By using the Pythagorean theorem, this representation can be interpreted geometrically: the Pythagorean primes are exactly the odd prime numbers p such that there exists a right triangle, with integer legs, whose hypotenuse has length √p. They are also exactly the prime numbers p such that there exists a right triangle with integer sides whose hypotenuse has length p. For, if the triangle with legs x and y has hypotenuse length √p (with x > y), then the triangle with legs x2 − y2 and 2xy has hypotenuse length p.[5]
Another way to understand this representation as a sum of two squares involves Gaussian integers, the complex numbers whose real part and imaginary part are both integers.[6] The norm of a Gaussian integer x + yi is the number x2 + y2. Thus, the Pythagorean primes (and 2) occur as norms of Gaussian integers, while other primes do not. Within the Gaussian integers, the Pythagorean primes are not considered to be prime numbers, because they can be factored as
Similarly, their squares can be factored in a different way than their integer factorization, as
The real and imaginary parts of the factors in these factorizations are the leg lengths of the right triangles having the given hypotenuses.
Quadratic residues[edit]
The law of quadratic reciprocity says that if p and q are distinct odd primes, at least one of which is Pythagorean, then p is a quadratic residue mod q if and only if q is a quadratic residue mod p; by contrast, if neither p nor q is Pythagorean, then p is a quadratic residue mod q if and only if q is not a quadratic residue mod p.[7]
In the finite field Z/p with p a Pythagorean prime, the polynomial equation x2 = −1 has two solutions. This may be expressed by saying that −1 is a quadratic residue mod p. In contrast, this equation has no solution in the finite fields Z/p where p is an odd prime but is not Pythagorean.[8]
For every Pythagorean prime p, there exists a Paley graph with p vertices, representing the numbers modulo p, with two numbers adjacent in the graph if and only if their difference is a quadratic residue. This definition produces the same adjacency relation regardless of the order in which the two numbers are subtracted to compute their difference, because of the property of Pythagorean primes that −1 is a quadratic residue.[9]
References[edit]
Unique factorization
Writing a number as a product of prime numbers is called a prime factorization of the number. For example:
The terms in the product are called prime factors. The same prime factor may occur more than once; this example has two copies of the prime factor When a prime occurs multiple times, exponentiation can be used to group together multiple copies of the same prime number: for example, in the second way of writing the product above, denotes the square or second power of
The central importance of prime numbers to number theory and mathematics in general stems from the fundamental theorem of arithmetic.[44] This theorem states that every integer larger than 1 can be written as a product of one or more primes. More strongly, this product is unique in the sense that any two prime factorizations of the same number will have the same numbers of copies of the same primes, although their ordering may differ.[45] So, although there are many different ways of finding a factorization using an integer factorization algorithm, they all must produce the same result. Primes can thus be considered the "basic building blocks" of the natural numbers.[46]
Some proofs of the uniqueness of prime factorizations are based on Euclid's lemma: If is a prime number and divides a product of integers and then divides or divides (or both).[47] Conversely, if a number has the property that when it divides a product it always divides at least one factor of the product, then must be prime.[48]
Algorithm[edit]
There is a trivial algorithm for decomposing a prime of the form into a sum of two squares: For all n such , test whether the square root of is an integer. If this the case, one has got the decomposition.
However the input size of the algorithm is the number of digits of p (up to a constant factor that depends on the numeral base). The number of needed tests is of the order of and thus exponential in the input size. So the computational complexity of this algorithm is exponential.
An algorithm with a polynomial complexity has been described by Stan Wagon in 1990, based on work by Serret and Hermite (1848), and Cornacchia (1908).[5]
History[edit]
Albert Girard was the first to make the observation, describing all positive integer numbers (not necessarily primes) expressible as the sum of two squares of positive integers; this was published in 1625.[2][3] The statement that every prime p of the form 4n+1 is the sum of two squares is sometimes called Girard's theorem.[4] For his part, Fermat wrote an elaborate version of the statement (in which he also gave the number of possible expressions of the powers of p as a sum of two squares) in a letter to Marin Mersenne dated December 25, 1640: for this reason this version of the theorem is sometimes called Fermat's Christmas theorem.
Gaussian primes[edit]
Fermat's theorem on sums of two squares is strongly related with the theory of Gaussian primes.
A Gaussian integer is a complex number such that a and b are integers. The norm of a Gaussian integer is an integer equal to the square of the absolute value of the Gaussian integer. The norm of a product of Gaussian integers is the product of their norms. This is the Diophantus identity, which results immediately from the similar property of the absolute value.
Gaussian integers form a principal ideal domain. This implies that Gaussian primes can be defined similarly as primes numbers, that is as those Gaussian integers that are not the product of two non-units (here the units are 1, −1, i and −i).
The multiplicative property of the norm implies that a prime number p is either a Gaussian prime or the norm of a Gaussian prime. Fermat's theorem asserts that the first case occurs when and that the second case occurs when and The last case is not considered in Fermat's statement, but is trivial, as
Arithmetic (from Ancient Greek ἀριθμός (arithmós) 'number', and τική [τέχνη] (tikḗ [tékhnē]) 'art, craft') is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today.Parity (mathematics)
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it isn't.[1] For example, −4, 0, 82 are even because
By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings.
Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even.[2] Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwise it is even—as the last digit of any even number is 0, 2, 4, 6, or 8. The same idea will work using any even base. In particular, a number expressed in the binary numeral system is odd if its last digit is 1; and it is even if its last digit is 0. In an odd base, the number is even according to the sum of its digits—it is even if and only if the sum of its digits is even.[3]
Cuisenaire rods
Cuisenaire rods are mathematics learning aids for students that provide an interactive, hands-on[1] way to explore mathematics and learn mathematical concepts, such as the four basic arithmetical operations, working with fractions and finding divisors.[2][3] In the early 1950s, Caleb Gattegno popularised this set of coloured number rods created by the Belgian primary school teacher Georges Cuisenaire (1891–1975), who called the rods réglettes.
According to Gattegno, "Georges Cuisenaire showed in the early 1950s that students who had been taught traditionally, and were rated 'weak', took huge strides when they shifted to using the material. They became 'very good' at traditional arithmetic when they were allowed to manipulate the rods."[4]
History[edit]
The educationalists Maria Montessori and Friedrich Fröbel[5] had used rods to represent numbers, but it was Georges Cuisenaire who introduced the rods that were to be used across the world from the 1950s onwards. In 1952 he published Les nombres en couleurs, Numbers in Color, which outlined their use. Cuisenaire, a violin player, taught music as well as arithmetic in the primary school in Thuin. He wondered why children found it easy and enjoyable to pick up a tune and yet found mathematics neither easy nor enjoyable. These comparisons with music and its representation led Cuisenaire to experiment in 1931 with a set of ten rods sawn out of wood, with lengths from 1 cm to 10 cm. He painted each length of rod a different colour and began to use these in his teaching of arithmetic. The invention remained almost unknown outside the village of Thuin for about 23 years until, in April 1953, British mathematician and mathematics education specialist Caleb Gattegno was invited to see students using the rods in Thuin. At this point he had already founded the International Commission for the Study and Improvement of Mathematics Education (CIEAEM) and the Association of Teachers of Mathematics, but this marked a turning point in his understanding:
Gattegno named the rods "Cuisenaire rods" and began trialing and popularizing them. Seeing that the rods allowed students "to expand on their latent mathematical abilities in a creative and enjoyable fashion", Gattegno's pedagogy shifted radically as he began to stand back and allow students to take a leading role:
While the material has found an important place in myriad teacher-centered lessons, Gattegno's student-centered practice also inspired a number of educators. The French-Canadian educator Madeleine Goutard in her 1963 Mathematics and Children, wrote:
John Holt, in his 1964 How Children Fail, wrote:
Gattegno formed the Cuisenaire Company in Reading, England, in 1954,[8] and by the end of the 1950s, Cuisenaire rods had been adopted by teachers in 10,000 schools in more than a hundred countries.[9] The rods received wide use in the 1960s and 1970s. In 2000, the United States-based company Educational Teaching Aids (ETA) acquired the US Cuisenaire Company and formed ETA/Cuisenaire to sell Cuisenaire rods-related material. In 2004, Cuisenaire rods were featured in an exhibition of paintings and sculptures by New Zealand artist Michael Parekowhai.
Rods[edit]
| Colour | Common abbreviation | Length (in centimetres) |
|---|---|---|
| White | w | 1 |
| Red | r | 2 |
| Light green | g | 3 |
| Purple (or pink) | p | 4 |
| Yellow | y | 5 |
| Dark green | d | 6 |
| Black | b | 7 |
| Brown (or "tan") | t | 8 |
| Blue | B | 9 |
| Orange | O | 10 |
Another arrangement, common in Eastern Europe, extended by two large (10+ cm) sizes of rods, is the following:
| Colour | Length (in centimetres) |
|---|---|
| White | 1 |
| Pink | 2 |
| Light blue | 3 |
| Red | 4 |
| Yellow | 5 |
| Purple | 6 |
| Black | 7 |
| Brown | 8 |
| Dark blue | 9 |
| Orange | 10 |
| Green | 12 |
| Tan | 16 |
Use in mathematics teaching[edit]
The rods are used in teaching a variety of mathematical ideas, and with a wide age range of learners.[10] Topics they are used for include:[10]
The Silent Way[edit]
Though primarily used for mathematics, they have also become popular in language-teaching classrooms, particularly The Silent Way.[11] They can be used
Other coloured rods[edit]
In her first school, and in schools since then, Maria Montessori used coloured rods in the classroom to teach concepts of both mathematics and length. This is possibly the first instance of coloured rods being used in the classroom for this purpose.
Catherine Stern also devised a set of coloured rods produced by staining wood with aesthetically pleasing colours, and published books on their use at around the same time as Cuisenaire and Gattegno.[14][15] Her rods were different colours to Cuisenaire's, and also larger, with a 2 cm unit cube rather than 1 cm. She produced various resources to complement the rods, such as trays to arrange the rods in, and tracks to arrange them on. Tony Wing, in producing resources for Numicon, built on many of Stern's ideas, also making trays and tracks available for use with Cuisenaire rods.[16]
In 1961 Seton Pollock produced the Colour Factor system,[17] consisting of rods from lengths 1 to 12 cm. Based on the work of Cuisenaire and Gattegno, he had invented a unified system for logically assigning a color to any number. After white (1), the primary colors red, blue and yellow are assigned to the first three primes (2, 3 and 5). Higher primes (7, 11 etc.) are associated with darkening shades of grey. The colors of non-prime numbers are obtained by mixing the colors associated with their factors – this is the key concept. A patent is registered in Pollock's name for an "Apparatus for teaching or studying mathematics".[18] The aesthetic and numerically comprehensive Color Factor system was marketed for some years by Seton Pollock's family, before being conveyed to Edward Arnold, the educational publishing house. The colors of Pollock's system were named distinctively using, for example, 'scarlet' instead of 'red', and 'amber' instead of 'orange'. They are listed below.[19]
| Colour | Length (in centimetres) |
|---|---|
| White | 1 |
| Pink | 2 |
| Light Blue | 3 |
| Scarlet | 4 |
| Yellow | 5 |
| Violet | 6 |
| Grey | 7 |
| Crimson | 8 |
| Royal Blue | 9 |
| Amber | 10 |
| Dark Grey | 11 |
| Mauve | 12 |
This one is the shit













































































Comments
Post a Comment
No Comment