Triangles

Posted by Tino Cogin of Samos June 06, 2023

Triangles

Triangles[edit]

All triangles are cyclic; that is, every triangle has a circumscribed circle.

Straightedge and compass construction[edit]

Construction of the circumcircle of triangle

△ ABC

and the circumcenter

Q

The circumcenter of a triangle can be constructed by drawing any two of the three perpendicular bisectors. For three non-collinear points, these two lines cannot be parallel, and the circumcenter is the point where they cross. Any point on the bisector is equidistant from the two points that it bisects, from which it follows that this point, on both bisectors, is equidistant from all three triangle vertices. The circumradius is the distance from it to any of the three vertices.

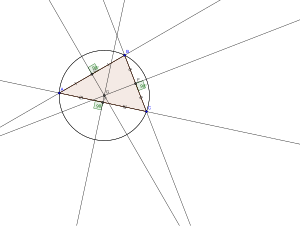
Alternative construction[edit]

Alternative construction of the circumcenter (intersection of broken lines)

An alternative method to determine the circumcenter is to draw any two lines each one departing from one of the vertices at an angle with the common side, the common angle of departure being 90° minus the angle of the opposite vertex. (In the case of the opposite angle being obtuse, drawing a line at a negative angle means going outside the triangle.)

In coastal navigation, a triangle's circumcircle is sometimes used as a way of obtaining a position line using a sextant when no compass is available. The horizontal angle between two landmarks defines the circumcircle upon which the observer lies.

Circumcircle equations[edit]

Cartesian coordinates[edit]

In the Euclidean plane, it is possible to give explicitly an equation of the circumcircle in terms of the Cartesian coordinates of the vertices of the inscribed triangle. Suppose that

{\begin{aligned}\mathbf {A} &=(A_{x},A_{y})\\\mathbf {B} &=(B_{x},B_{y})\\\mathbf {C} &=(C_{x},C_{y})\end{aligned}}

are the coordinates of points $A, B, C$ . The circumcircle is then the locus of points $\mathbf {v} =(v_{x},v_{y})$ in the Cartesian plane satisfying the equations

{\begin{aligned}|\mathbf {v} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {A} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {B} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {C} -\mathbf {u} |^{2}&=r^{2}\end{aligned}}

guaranteeing that the points $A, B, C, v$ are all the same distance $r$ from the common center $\mathbf {u}$ of the circle. Using the polarization identity, these equations reduce to the condition that the matrix

{\begin{bmatrix}|\mathbf {v} |^{2}&-2v_{x}&-2v_{y}&-1\\|\mathbf {A} |^{2}&-2A_{x}&-2A_{y}&-1\\|\mathbf {B} |^{2}&-2B_{x}&-2B_{y}&-1\\|\mathbf {C} |^{2}&-2C_{x}&-2C_{y}&-1\end{bmatrix}}

has a nonzero kernel. Thus the circumcircle may alternatively be described as the locus of zeros of the determinant of this matrix:

\det {\begin{bmatrix}|\mathbf {v} |^{2}&v_{x}&v_{y}&1\\|\mathbf {A} |^{2}&A_{x}&A_{y}&1\\|\mathbf {B} |^{2}&B_{x}&B_{y}&1\\|\mathbf {C} |^{2}&C_{x}&C_{y}&1\end{bmatrix}}=0.

Using cofactor expansion, let

{\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}

we then have $a|\mathbf {v} |^{2}-2\mathbf {Sv} -b=0$ where $\mathbf {S} =(S_{x},S_{y}),$ and – assuming the three points were not in a line (otherwise the circumcircle is that line that can also be seen as a generalized circle with $S$ at infinity) – $\left|\mathbf {v} -{\tfrac {\mathbf {S} }{a}}\right|^{2}={\tfrac {b}{a}}+{\tfrac {|\mathbf {S} |^{2}}{a^{2}}},$ giving the circumcenter ${\tfrac {\mathbf {S} }{a}}$ and the circumradius ${\sqrt {{\tfrac {b}{a}}+{\tfrac {|\mathbf {S} |^{2}}{a^{2}}}}}.$ A similar approach allows one to deduce the equation of the circumsphere of a tetrahedron.