Angular moment of moments

Examples[edit]

The trivial case of the angular momentum ${\displaystyle 𝐿}$ of a body in an orbit is given by

$${\displaystyle 𝐿=2𝜋𝑀𝑓{𝑟}^2}$$

where ${\displaystyle 𝑀}$ is the mass of the orbiting object, ${\displaystyle 𝑓}$ is the orbit's frequency and ${\displaystyle 𝑟}$ is the orbit's radius.

The angular momentum ${\displaystyle 𝐿}$ of a uniform rigid sphere rotating around its axis, instead, is given by

$${\displaystyle 𝐿=\frac{4}{5}𝜋𝑀𝑓{𝑟}^2}$$

where ${\displaystyle 𝑀}$ is the sphere's mass, ${\displaystyle 𝑓}$ is the frequency of rotation and ${\displaystyle 𝑟}$ is the sphere's radius.

Thus, for example, the orbital angular momentum of the Earth with respect to the Sun is about 2.66 × 10⁴⁰ kg⋅m²⋅s⁻¹, while its rotational angular momentum is about 7.05 × 10³³ kg⋅m²⋅s⁻¹.

In the case of a uniform rigid sphere rotating around its axis, if, instead of its mass, its density is known, the angular momentum ${\displaystyle 𝐿}$ is given by

$${\displaystyle 𝐿=\frac{16}{15}{𝜋}^2𝜌𝑓{𝑟}^5}$$

where ${\displaystyle 𝜌}$ is the sphere's density, ${\displaystyle 𝑓}$ is the frequency of rotation and ${\displaystyle 𝑟}$ is the sphere's radius.

In the simplest case of a spinning disk, the angular momentum ${\displaystyle 𝐿}$ is given by^[4]

$${\displaystyle 𝐿=𝜋𝑀𝑓{𝑟}^2}$$

where ${\displaystyle 𝑀}$ is the disk's mass, ${\displaystyle 𝑓}$ is the frequency of rotation and ${\displaystyle 𝑟}$ is the disk's radius.

If instead the disk rotates about its diameter (e.g. coin toss), its angular momentum ${\displaystyle 𝐿}$ is given by^[4]

$${\displaystyle 𝐿=\frac{1}{2}𝜋𝑀𝑓{𝑟}^2}$$

Just as for angular velocity, there are two special types of angular momentum of an object: the spin angular momentum is the angular momentum about the object's centre of mass, while the orbital angular momentum is the angular momentum about a chosen center of rotation. The Earth has an orbital angular momentum by nature of revolving around the Sun, and a spin angular momentum by nature of its daily rotation around the polar axis. The total angular momentum is the sum of the spin and orbital angular momenta. In the case of the Earth the primary conserved quantity is the total angular momentum of the solar system because angular momentum is exchanged to a small but important extent among the planets and the Sun. The orbital angular momentum vector of a point particle is always parallel and directly proportional to its orbital angular velocity vector ω, where the constant of proportionality depends on both the mass of the particle and its distance from origin. The spin angular momentum vector of a rigid body is proportional but not always parallel to the spin angular velocity vector Ω, making the constant of proportionality a second-rank tensor rather than a scalar.

Orbital angular momentum in two dimensions[edit]

Velocity of the particle m with respect to the origin O can be resolved into components parallel to (v_∥) and perpendicular to (v_⊥) the radius vector r. The angular momentum of m is proportional to the perpendicular component v_⊥ of the velocity, or equivalently, to the perpendicular distance r_⊥ from the origin.

Angular momentum is a vector quantity (more precisely, a pseudovector) that represents the product of a body's rotational inertia and rotational velocity (in radians/sec) about a particular axis. However, if the particle's trajectory lies in a single plane, it is sufficient to discard the vector nature of angular momentum, and treat it as a scalar (more precisely, a pseudoscalar).^[5] Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum p is proportional to mass m and linear speed v,

$${\displaystyle 𝑝=𝑚𝑣,}$$

angular momentum L is proportional to moment of inertia I and angular speed ω measured in radians per second.^[6]

$${\displaystyle 𝐿=𝐼𝜔.}$$

Unlike mass, which depends only on amount of matter, moment of inertia depends also on the position of the axis of rotation and the distribution of the matter. Unlike linear velocity, which does not depend upon the choice of origin, orbital angular velocity is always measured with respect to a fixed origin. Therefore, strictly speaking, L should be referred to as the angular momentum relative to that center.^[7]

In the case of circular motion of a single particle, we can use ${\displaystyle 𝐼={𝑟}^2𝑚}$ and ${\displaystyle 𝜔=𝑣/𝑟}$ to expand angular momentum as ${\displaystyle 𝐿={𝑟}^2𝑚\cdot 𝑣/𝑟,}$ reducing to:

$${\displaystyle 𝐿=𝑟𝑚𝑣,}$$

the product of the radius of rotation r and the linear momentum of the particle ${\displaystyle 𝑝=𝑚𝑣}$, where ${\displaystyle 𝑣=𝑟𝜔}$ is the linear (tangential) speed.

This simple analysis can also apply to non-circular motion if one uses the component of the motion perpendicular to the radius vector:

$${\displaystyle 𝐿=𝑟𝑚{𝑣}_{\perp },}$$

where ${\displaystyle {𝑣}_{\perp }=𝑣\sin (𝜃)}$ is the perpendicular component of the motion. Expanding, ${\displaystyle 𝐿=𝑟𝑚𝑣\sin (𝜃),}$ rearranging, ${\displaystyle 𝐿=𝑟\sin (𝜃)𝑚𝑣,}$ and reducing, angular momentum can also be expressed,

$${\displaystyle 𝐿={𝑟}_{\perp }𝑚𝑣,}$$

where ${\displaystyle {𝑟}_{\perp }=𝑟\sin (𝜃)}$ is the length of the moment arm, a line dropped perpendicularly from the origin onto the path of the particle. It is this definition, (length of moment arm) × (linear momentum), to which the term moment of momentum refers.^[8]

Orbital angular momentum in three dimensions[edit]

Relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. r is the position vector.

To completely define orbital angular momentum in three dimensions, it is required to know the rate at which the position vector sweeps out angle, the direction perpendicular to the instantaneous plane of angular displacement, and the mass involved, as well as how this mass is distributed in space.^[9] By retaining this vector nature of angular momentum, the general nature of the equations is also retained, and can describe any sort of three-dimensional motion about the center of rotation – circular, linear, or otherwise. In vector notation, the orbital angular momentum of a point particle in motion about the origin can be expressed as:

$${\displaystyle \mathbf{𝐿}=𝐼\mathit{𝜔},}$$

where

• ${\displaystyle 𝐼={𝑟}^2𝑚}$ is the moment of inertia for a point mass,
• ${\displaystyle \mathit{𝜔}=\frac{\mathbf{𝑟}\times \mathbf{𝑣}}{{𝑟}^2}}$ is the orbital angular velocity of the particle about the origin,
• ${\displaystyle \mathbf{𝑟}}$ is the position vector of the particle relative to the origin, and ${\displaystyle 𝑟=\left|\mathbf{𝑟}\right|}$,
• ${\displaystyle \mathbf{𝑣}}$ is the linear velocity of the particle relative to the origin, and
• ${\displaystyle 𝑚}$ is the mass of the particle.

Analogy to linear momentum[edit]

Angular momentum can be described as the rotational analog of linear momentum. Like linear momentum it involves elements of mass and displacement. Unlike linear momentum it also involves elements of position and shape.

Many problems in physics involve matter in motion about some certain point in space, be it in actual rotation about it, or simply moving past it, where it is desired to know what effect the moving matter has on the point—can it exert energy upon it or perform work about it? Energy, the ability to do work, can be stored in matter by setting it in motion—a combination of its inertia and its displacement. Inertia is measured by its mass, and displacement by its velocity. Their product,

is the matter's momentum.^[10] Referring this momentum to a central point introduces a complication: the momentum is not applied to the point directly. For instance, a particle of matter at the outer edge of a wheel is, in effect, at the end of a lever of the same length as the wheel's radius, its momentum turning the lever about the center point. This imaginary lever is known as the moment arm. It has the effect of multiplying the momentum's effort in proportion to its length, an effect known as a moment. Hence, the particle's momentum referred to a particular point,

is the angular momentum, sometimes called, as here, the moment of momentum of the particle versus that particular center point. The equation ${\displaystyle 𝐿=𝑟𝑚𝑣}$ combines a moment (a mass ${\displaystyle 𝑚}$ turning moment arm ${\displaystyle 𝑟}$) with a linear (straight-line equivalent) speed ${\displaystyle 𝑣}$. Linear speed referred to the central point is simply the product of the distance ${\displaystyle 𝑟}$ and the angular speed ${\displaystyle 𝜔}$ versus the point: ${\displaystyle 𝑣=𝑟𝜔,}$ another moment. Hence, angular momentum contains a double moment: ${\displaystyle 𝐿=𝑟𝑚𝑟𝜔.}$ Simplifying slightly, ${\displaystyle 𝐿={𝑟}^2𝑚𝜔,}$ the quantity ${\displaystyle {𝑟}^2𝑚}$ is the particle's moment of inertia, sometimes called the second moment of mass. It is a measure of rotational inertia.^[11]

Moment of inertia (shown here), and therefore angular momentum, is different for each shown configuration of mass and axis of rotation.

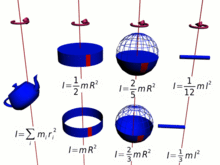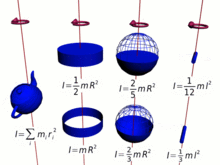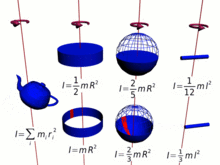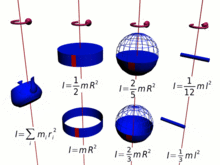
The above analogy of the translational momentum and rotational momentum can be expressed in vector form:^{[citation needed]}

• $\mathbf{𝑝}=𝑚\mathbf{𝑣}$ for linear motion
• ${\displaystyle \mathbf{𝐿}=𝐼\mathit{𝜔}}$ for rotation

The direction of momentum is related to the direction of the velocity for linear movement. The direction of angular momentum is related to the angular velocity of the rotation.

Because moment of inertia is a crucial part of the spin angular momentum, the latter necessarily includes all of the complications of the former, which is calculated by multiplying elementary bits of the mass by the squares of their distances from the center of rotation.^[12] Therefore, the total moment of inertia, and the angular momentum, is a complex function of the configuration of the matter about the center of rotation and the orientation of the rotation for the various bits.

For a rigid body, for instance a wheel or an asteroid, the orientation of rotation is simply the position of the rotation axis versus the matter of the body. It may or may not pass through the center of mass, or it may lie completely outside of the body. For the same body, angular momentum may take a different value for every possible axis about which rotation may take place.^[13] It reaches a minimum when the axis passes through the center of mass.^[14]

For a collection of objects revolving about a center, for instance all of the bodies of the Solar System, the orientations may be somewhat organized, as is the Solar System, with most of the bodies' axes lying close to the system's axis. Their orientations may also be completely random.

In brief, the more mass and the farther it is from the center of rotation (the longer the moment arm), the greater the moment of inertia, and therefore the greater the angular momentum for a given angular velocity. In many cases the moment of inertia, and hence the angular momentum, can be simplified by,^[15]

$${\displaystyle 𝐼={𝑘}^2𝑚,}$$

where ${\displaystyle 𝑘}$ is the radius of gyration, the distance from the axis at which the entire mass ${\displaystyle 𝑚}$ may be considered as concentrated.

For a planet, angular momentum is distributed between the spin of the planet and its revolution in its orbit, and these are often exchanged by various mechanisms. The conservation of angular momentum in the Earth–Moon system results in the transfer of angular momentum from Earth to Moon, due to tidal torque the Moon exerts on the Earth. This in turn results in the slowing down of the rotation rate of Earth, at about 65.7 nanoseconds per day,^[23] and in gradual increase of the radius of Moon's orbit, at about 3.82 centimeters per year.^[24]

The torque caused by the two opposing forces F_g and −F_g causes a change in the angular momentum L in the direction of that torque (since torque is the time derivative of angular momentum). This causes the top to precess.

The conservation of angular momentum explains the angular acceleration of an ice skater as they bring their arms and legs close to the vertical axis of rotation. By bringing part of the mass of their body closer to the axis, they decrease their body's moment of inertia. Because angular momentum is the product of moment of inertia and angular velocity, if the angular momentum remains constant (is conserved), then the angular velocity (rotational speed) of the skater must increase.

The same phenomenon results in extremely fast spin of compact stars (like white dwarfs, neutron stars and black holes) when they are formed out of much larger and slower rotating stars.

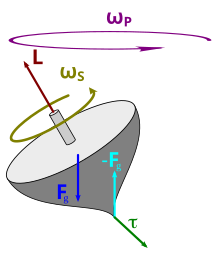
Conservation is not always a full explanation for the dynamics of a system but is a key constraint. For example, a spinning top is subject to gravitational torque making it lean over and change the angular momentum about the nutation axis, but neglecting friction at the point of spinning contact, it has a conserved angular momentum about its spinning axis, and another about its precession axis. Also, in any planetary system, the planets, star(s), comets, and asteroids can all move in numerous complicated ways, but only so that the angular momentum of the system is conserved.

Noether's theorem states that every conservation law is associated with a symmetry (invariant) of the underlying physics. The symmetry associated with conservation of angular momentum is rotational invariance. The fact that the physics of a system is unchanged if it is rotated by any angle about an axis implies that angular momentum is conserved.^[25]

Lorentz force law as the definition of E and B[edit]

Trajectory of a particle with a positive or negative charge q under the influence of a magnetic field B, which is directed perpendicularly out of the screen.

Beam of electrons moving in a circle, due to the presence of a magnetic field. Purple light revealing the electron's path in this Teltron tube is created by the electrons colliding with gas molecules.

Charged particles experiencing the Lorentz force.

In many textbook treatments of classical electromagnetism, the Lorentz force law is used as the definition of the electric and magnetic fields E and B.^[7][8][9] To be specific, the Lorentz force is understood to be the following empirical statement:

The electromagnetic force F on a test charge at a given point and time is a certain function of its charge q and velocity v, which can be parameterized by exactly two vectors E and B, in the functional form:

$${\displaystyle \mathbf{𝐹}=𝑞(\mathbf{𝐸}+\mathbf{𝑣}\times \mathbf{𝐵})}$$

This is valid, even for particles approaching the speed of light (that is, magnitude of v, |v| ≈ c).^[10] So the two vector fields E and B are thereby defined throughout space and time, and these are called the "electric field" and "magnetic field". The fields are defined everywhere in space and time with respect to what force a test charge would receive regardless of whether a charge is present to experience the force.

As a definition of E and B, the Lorentz force is only a definition in principle because a real particle (as opposed to the hypothetical "test charge" of infinitesimally-small mass and charge) would generate its own finite E and B fields, which would alter the electromagnetic force that it experiences.^[11] In addition, if the charge experiences acceleration, as if forced into a curved trajectory, it emits radiation that causes it to lose kinetic energy. See for example Bremsstrahlung and synchrotron light. These effects occur through both a direct effect (called the radiation reaction force) and indirectly (by affecting the motion of nearby charges and currents).

Equation[edit]

Charged particle[edit]

Lorentz force F on a charged particle (of charge q) in motion (instantaneous velocity v). The E field and B field vary in space and time.

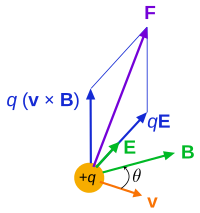
The force F acting on a particle of electric charge q with instantaneous velocity v, due to an external electric field E and magnetic field B, is given by (in SI units^[1]):^[12]

${\displaystyle \mathbf{𝐹}=𝑞\left(\mathbf{𝐸}+\mathbf{𝑣}\times \mathbf{𝐵}\right)}$

where × is the vector cross product (all boldface quantities are vectors). In terms of Cartesian components, we have:

In general, the electric and magnetic fields are functions of the position and time. Therefore, explicitly, the Lorentz force can be written as:

$${\displaystyle \mathbf{𝐹}\left(\mathbf{𝑟}(𝑡),\dot{\mathbf{𝑟}}(𝑡),𝑡,𝑞\right)=𝑞\left[\mathbf{𝐸}(\mathbf{𝑟},𝑡)+\dot{\mathbf{𝑟}}(𝑡)\times \mathbf{𝐵}(\mathbf{𝑟},𝑡)\right]}$$

in which r is the position vector of the charged particle, t is time, and the overdot is a time derivative.

A positively charged particle will be accelerated in the same linear orientation as the E field, but will curve perpendicularly to both the instantaneous velocity vector v and the B field according to the right-hand rule (in detail, if the fingers of the right hand are extended to point in the direction of v and are then curled to point in the direction of B, then the extended thumb will point in the direction of F).

The term qE is called the electric force, while the term q(v × B) is called the magnetic force.^[13] According to some definitions, the term "Lorentz force" refers specifically to the formula for the magnetic force,^[14] with the total electromagnetic force (including the electric force) given some other (nonstandard) name. This article will not follow this nomenclature: In what follows, the term "Lorentz force" will refer to the expression for the total force.

The magnetic force component of the Lorentz force manifests itself as the force that acts on a current-carrying wire in a magnetic field. In that context, it is also called the Laplace force.

The Lorentz force is a force exerted by the electromagnetic field on the charged particle, that is, it is the rate at which linear momentum is transferred from the electromagnetic field to the particle. Associated with it is the power which is the rate at which energy is transferred from the electromagnetic field to the particle. That power is

$${\displaystyle \mathbf{𝑣}\cdot \mathbf{𝐹}=𝑞\mathbf{𝑣}\cdot \mathbf{𝐸}.}$$

Notice that the magnetic field does not contribute to the power because the magnetic force is always perpendicular to the velocity of the particle.

Inverse-square law

31 languages

• Article
• Talk

• Read
• Edit
• View history

Tools

From Wikipedia, the free encyclopedia

S represents the light source, while r represents the measured points. The lines represent the flux emanating from the sources and fluxes. The total number of flux lines depends on the strength of the light source and is constant with increasing distance, where a greater density of flux lines (lines per unit area) means a stronger energy field. The density of flux lines is inversely proportional to the square of the distance from the source because the surface area of a sphere increases with the square of the radius. Thus the field intensity is inversely proportional to the square of the distance from the source.

In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

Radar energy expands during both the signal transmission and the reflected return, so the inverse square for both paths means that the radar will receive energy according to the inverse fourth power of the range.

To prevent dilution of energy while propagating a signal, certain methods can be used such as a waveguide, which acts like a canal does for water, or how a gun barrel restricts hot gas expansion to one dimension in order to prevent loss of energy transfer to a bullet.

The inverse-square law generally applies when some force, energy, or other conserved quantity is evenly radiated outward from a point source in three-dimensional space. Since the surface area of a sphere (which is 4πr²) is proportional to the square of the radius, as the emitted radiation gets farther from the source, it is spread out over an area that is increasing in proportion to the square of the distance from the source. Hence, the intensity of radiation passing through any unit area (directly facing the point source) is inversely proportional to the square of the distance from the point source. Gauss's law for gravity is similarly applicable, and can be used with any physical quantity that acts in accordance with the inverse-square relationship.