ΘοΔΣΣ

The energy required to break one mole of hydrogen-hydrogen bonds in H2 is 436 kJ. What is the longest wavelength of light with sufficient energy to break a single hydrogen-hydrogen bond? A. 122 nm B. 132 nm C. 275 nm D. 656 nm

Wavelength:

The relationship between the energy, the wavelength is given by the Planck's equation. It is also referred to as the photon energy which denotes the energy required to excite a photon(light) from its ground state. It is given by $E={\displaystyle \frac{hc}{\lambda }}$

Answer and Explanation:

It is given that the energy required to break one mole of hydrogen-hydrogen bonds in H2 is 436 kJ.

So, one mole of H2 contains Avogadro's number of...

See full answer below

An electrode is an electrical conductor used to make contact with a nonmetallic part of a circuit (e.g. a semiconductor, an electrolyte, a vacuum or air). Electrodes are essential parts of batteries that can consist of a variety of materials (chemicals) depending on the type of battery.

The electrophore, invented by Johan Wilcke, was an early version of an electrode used to study static electricity.^[1]

Anode and cathode in electrochemical cells

[edit]

Schematic of a voltaic (galvanic) cell

Electrodes are an essential part of any battery. The first electrochemical battery was devised by Alessandro Volta and was aptly named the Voltaic cell.^[2] This battery consisted of a stack of copper and zinc electrodes separated by brine-soaked paper disks. Due to fluctuation in the voltage provided by the voltaic cell, it was not very practical. The first practical battery was invented in 1839 and named the Daniell cell after John Frederic Daniell. It still made use of the zinc–copper electrode combination. Since then, many more batteries have been developed using various materials. The basis of all these is still using two electrodes, anodes and cathodes.

Anode (-)

[edit]

'Anode' was coined by William Whewell at Michael Faraday's request, derived from the Greek words ἄνο (ano), 'upwards' and ὁδός (hodós), 'a way'.^[3] The anode is the electrode through which the conventional current enters from the electrical circuit of an electrochemical cell (battery) into the non-metallic cell. The electrons then flow to the other side of the battery. Benjamin Franklin surmised that the electrical flow moved from positive to negative.^[4] The electrons flow away from the anode and the conventional current towards it. From both can be concluded that the charge of the anode is negative. The electron entering the anode comes from the oxidation reaction that takes place next to it.

Cathode (+)

[edit]

The cathode is in many ways the opposite of the anode. The name (also coined by Whewell) comes from the Greek words κάτω (kato), 'downwards' and ὁδός (hodós), 'a way'. It is the positive electrode, meaning the electrons flow from the electrical circuit through the cathode into the non-metallic part of the electrochemical cell. At the cathode, the reduction reaction takes place with the electrons arriving from the wire connected to the cathode and are absorbed by the oxidizing agent.

In physics, Planck's law (also Planck radiation law^[1]: 1305) describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.^[2]

At the end of the 19th century, physicists were unable to explain why the observed spectrum of black-body radiation, which by then had been accurately measured, diverged significantly at higher frequencies from that predicted by existing theories. In 1900, German physicist Max Planck heuristically derived a formula for the observed spectrum by assuming that a hypothetical electrically charged oscillator in a cavity that contained black-body radiation could only change its energy in a minimal increment, E, that was proportional to the frequency of its associated electromagnetic wave. While Planck originally regarded the hypothesis of dividing energy into increments as a mathematical artifice, introduced merely to get the correct answer, other physicists including Albert Einstein built on his work, and Planck's insight is now recognized to be of fundamental importance to quantum theory.

h is the Planck constant, and c is the speed of light in the medium, whether material or

E=hc/λ

The Planck constant, or Planck's constant, denoted by $h$,^[1] is a fundamental physical constant^[1] of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum.

The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation.^[2] Planck later referred to the constant as the "quantum of action".^[3] In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".

In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass.^[4] The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value

 ${\displaystyle h}$ = 6.62607015×10⁻³⁴ J⋅Hz⁻¹.^[5][6]

         = 4.135667696...×10⁻¹⁵ eV⋅Hz⁻¹

In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.^[1][2] In other words, it is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings. Wavelength is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns.^[3][4] The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter lambda (λ). The term "wavelength" is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.^[5]

Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to the frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.^[6]

Wavelength depends on the medium (for example, vacuum, air, or water) that a wave travels through. Examples of waves are sound waves, light, water waves and periodic electrical signals in a conductor. A sound wave is a variation in air pressure, while in light and other electromagnetic radiation the strength of the electric and the magnetic field vary. Water waves are variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary.

The range of wavelengths or frequencies for wave phenomena is called a spectrum. The name originated with the visible light spectrum but now can be applied to the entire electromagnetic spectrum as well as to a sound spectrum or vibration spectrum.

Conventions

The electrons, the charge carriers in an electrical circuit, flow in the opposite direction of the conventional electric current.

The symbol for a battery in a circuit diagram.

The conventional direction of current, also known as conventional current,^[16][17] is arbitrarily defined as the direction in which positive charges flow. In a conductive material, the moving charged particles that constitute the electric current are called charge carriers. In metals, which make up the wires and other conductors in most electrical circuits, the positively charged atomic nuclei of the atoms are held in a fixed position, and the negatively charged electrons are the charge carriers, free to move about in the metal. In other materials, notably the semiconductors, the charge carriers can be positive or negative, depending on the dopant used. Positive and negative charge carriers may even be present at the same time, as happens in an electrolyte in an electrochemical cell.

A flow of positive charges gives the same electric current, and has the same effect in a circuit, as an equal flow of negative charges in the opposite direction. Since current can be the flow of either positive or negative charges, or both, a convention is needed for the direction of current that is independent of the type of charge carriers. Negatively charged carriers, such as the electrons (the charge carriers in metal wires and many other electronic circuit components), therefore flow in the opposite direction of conventional current flow in an electrical circuit.^[16][17]

Reference direction

A current in a wire or circuit element can flow in either of two directions. When defining a variable ${\displaystyle I}$ to represent the current, the direction representing positive current must be specified, usually by an arrow on the circuit schematic diagram.^{[18][19]: 13} This is called the reference direction of the current ${\displaystyle I}$. When analyzing electrical circuits, the actual direction of current through a specific circuit element is usually unknown until the analysis is completed. Consequently, the reference directions of currents are often assigned arbitrarily. When the circuit is solved, a negative value for the current implies the actual direction of current through that circuit element is opposite that of the chosen reference direction.^[a]: 29

Sinusoidal waves

[edit]

In linear media, any wave pattern can be described in terms of the independent propagation of sinusoidal components. The 

wavelength λ of a sinusoidal waveform traveling

 at constant speed ${\displaystyle v}$ is given by^[7]

${\displaystyle \lambda =\frac{v}{f},}$

In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier transform) of the structure repeat per unit of distance.

The SI unit of spatial frequency is the reciprocal metre (m⁻¹),^[1] although cycles per meter (c/m) is also common. In image-processing applications, spatial frequency is often expressed in units of cycles per millimeter (c/mm) or also line pairs per millimeter (LP/mm).

In wave propagation, the spatial frequency is also known as wavenumber. Ordinary wavenumber is defined as the reciprocal of wavelength ${\displaystyle \lambda }$ and is commonly denoted by ${\displaystyle \xi }$^[2] or sometimes ${\displaystyle \nu }$:^[3]$${\displaystyle \xi =\frac{1}{\lambda }.}$$Angular wavenumber ${\displaystyle k}$, expressed in radian per metre (rad/m), is related to ordinary wavenumber and wavelength by$${\displaystyle k=2\pi \xi =\frac{2\pi }{\lambda }.}$$

Visual perception

[edit]

In the study of visual perception, sinusoidal gratings are frequently used to probe the capabilities of the visual system, such as contrast sensitivity. In these stimuli, spatial frequency is expressed as the number of cycles per degree of visual angle. Sine-wave gratings also differ from one another in amplitude (the magnitude of difference in intensity between light and dark stripes), orientation, and phase.

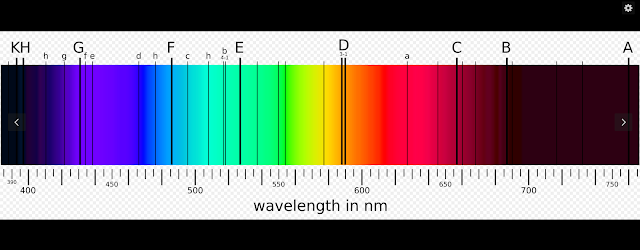
The Fraunhofer lines are a set of spectral absorption lines. They are dark absorption lines, seen in the optical spectrum of the Sun, and are formed when atoms in the solar atmosphere absorb light being emitted by the solar photosphere. The lines are named after German physicist Joseph von Fraunhofer, who observed them in 1814.

Discovery

[edit]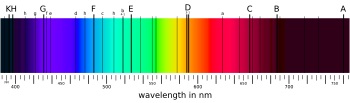

Solar spectrum with Fraunhofer lines as it appears visually.

In 1802, English chemist William Hyde Wollaston^[2] was the first person to note the appearance of a number of dark features in the solar spectrum.^[3] In 1814, Joseph von Fraunhofer independently rediscovered the lines and began to systematically study and measure their wavelengths. He mapped over 570 lines, designating the most prominent with the letters A through K and weaker lines with other letters.^[4][5][6] Modern observations of sunlight can detect many thousands of lines.

About 45 years later, Gustav Kirchhoff and Robert Bunsen^[7] noticed that several Fraunhofer lines coincide with characteristic emission lines identified in the spectra of heated chemical elements.^[8] They inferred that dark lines in the solar spectrum are caused by absorption by chemical elements in the solar atmosphere.^[9] Some of the observed features were identified as telluric lines originating from absorption by oxygen molecules in the Earth's atmosphere.

In the 6th century BC, the ancient Greek philosopher Pythagoras wanted to know why some combinations of musical sounds seemed more beautiful than others, and he found answers in terms of numerical ratios representing the harmonic overtone series on a string. He is reputed to have observed that when the lengths of vibrating strings are expressible as ratios of integers (e.g. 2 to 3, 3 to 4), the tones produced will be harmonious, and the smaller the integers the more harmonious the sounds. For example, a string of a certain length would sound particularly harmonious with a string of twice the length (other factors being equal). In modern parlance, if a string sounds the note C when plucked, a string twice as long will sound a C an octave lower. In one system of musical tuning, the tones in between are then given by 16:9 for D, 8:5 for E, 3:2 for F, 4:3 for G, 6:5 for A, and 16:15 for B, in ascending order.^[6]

The hydrogen line, 21 centimeter line, or H I line^[a] is a spectral line that is created by a change in the energy state of solitary, electrically neutral hydrogen atoms. It is produced by a spin-flip transition, which means the direction of the electron's spin is reversed relative to the spin of the proton. This is a quantum state change between the two hyperfine levels of the hydrogen 1 s ground state. The electromagnetic radiation producing this line has a frequency of 1420.405751768(2) MHz (1.42 GHz),^[1] which is equivalent to a wavelength of 21.106114054160(30) cm in a vacuum. According to the Planck–Einstein relation E = hν, the photon emitted by this transition has an energy of 5.8743261841116(81) μeV [9.411708152678(13)×10⁻²⁵ J]. The constant of proportionality, h, is known as the Planck constant.

The hydrogen line frequency lies in the L band, which is located in the lower end of the microwave region of the electromagnetic spectrum. It is frequently observed in radio astronomy because those radio waves can penetrate the large clouds of interstellar cosmic dust that are opaque to visible light. The existence of this line was predicted by Dutch astronomer H. van de Hulst in 1944, then directly observed by E. M. Purcell and his student H. E. Ewen in 1951. Observations of the hydrogen line have been used to reveal the spiral shape of the Milky Way, to calculate the mass and dynamics of individual galaxies, and to test for changes to the fine-structure constant over time. It is of particular importance to cosmology because it can be used to study the early Universe. Due to its fundamental properties, this line is of interest in the search for extraterrestrial intelligence. This line is the theoretical basis of the hydrogen maser.

n atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887,^[1][2] laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.^[3]

Background

[edit]

Gross structure

[edit]

The gross structure of line spectra is the structure predicted by the quantum mechanics of non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy levels only depend on the principal quantum number n. However, a more accurate model takes into account relativistic and spin effects, which break the degeneracy of the energy levels and split the spectral lines. The scale of the fine structure splitting relative to the gross structure energies is on the order of (Zα)², where Z is the atomic number and α is the fine-structure constant, a dimensionless number equal to approximately 1/137.

A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca⁺ and Sr⁺ and other ions such as He⁺, Li²⁺, and Be³⁺ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.

The non-relativistic Schrödinger equation and relativistic Dirac equation for the hydrogen atom can be solved analytically, owing to the simplicity of the two-particle physical system. The one-electron wave function solutions are referred to as hydrogen-like atomic orbitals. Hydrogen-like atoms are of importance because their corresponding orbitals bear similarity to the hydrogen atomic orbitals.

Other systems may also be referred to as "hydrogen-like atoms", such as muonium (an electron orbiting an antimuon), positronium (an electron and a positron), certain exotic atoms (formed with other particles), or Rydberg atoms (in which one electron is in such a high energy state that it sees the rest of the atom effectively as a point charge).

Schrödinger solution

[edit]

In the solution to the Schrödinger equation, which is non-relativistic, hydrogen-like atomic orbitals are eigenfunctions of the one-electron angular momentum operator L and its z component L_z. A hydrogen-like atomic orbital is uniquely identified by the values of the principal quantum number n, the angular momentum quantum number l, and the magnetic quantum number m. The energy eigenvalues do not depend on l or m, but solely on n. To these must be added the two-valued spin quantum number m_s = ±1⁄2, setting the stage for the Aufbau principle. This principle restricts the allowed values of the four quantum numbers in electron configurations of more-electron atoms. In hydrogen-like atoms all degenerate orbitals of fixed n and l, m and s varying between certain values (see below) form an atomic shell.

In atomic physics, a magnetic quantum number is a quantum number used to distinguish quantum states of an electron or other particle according to its angular momentum along a given axis in space. The orbital magnetic quantum number (m_l or m^[a]) distinguishes the orbitals available within a given subshell of an atom. It specifies the component of the orbital angular momentum that lies along a given axis, conventionally called the z-axis, so it describes the orientation of the orbital in space. The spin magnetic quantum number m_s specifies the z-axis component of the spin angular momentum for a particle having spin quantum number s. For an electron, s is 1⁄2, and m_s is either +1⁄2 or −1⁄2, often called "spin-up" and "spin-down", or α and β.^[1][2] The term magnetic in the name refers to the magnetic dipole moment associated with each type of angular momentum, so states having different magnetic quantum numbers shift in energy in a magnetic field according to the Zeeman effect.^[2]

The four quantum numbers conventionally used to describe the quantum state of an electron in an atom are the principal quantum number n, the azimuthal (orbital) quantum number ${\displaystyle \ell }$, and the magnetic quantum numbers m_l and m_s. Electrons in a given subshell of an atom (such as s, p, d, or f) are defined by values of ${\displaystyle \ell }$ (0, 1, 2, or 3). The orbital magnetic quantum number takes integer values in the range from ${\displaystyle -\ell }$ to ${\displaystyle +\ell }$, including zero.^[3] Thus the s, p, d, and f subshells contain 1, 3, 5, and 7 orbitals each. Each of these orbitals can accommodate up to two electrons (with opposite spins), forming the basis of the periodic table.

Other magnetic quantum numbers are similarly defined, such as m_j for the z-axis component the total electronic angular momentum j,^[1] and m_I for the nuclear spin I.^[2] Magnetic quantum numbers are capitalized to indicate totals for a system of particles, such as M_L or m_L for the total z-axis orbital angular momentum of all the electrons in an atom.^[2]

A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927.^[2] Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.^[3]