Hypotrochoids

Agree that:

 Electric is the idea of Motion Stored by Its~~~self as

Static Electric aka ANY Ba tt ~er Y

Moving itself as Magnetism ((=)) 

The Double Bubble 

bonding Helium

into He

As

The

Four C S 

S~C~Re~W

 EVIL

OUT OpH ((=)) InT(-)

LIFE

The Magnetic ((+)) form IN G Θ is G~iven the name Theta

Adding T to Eta by 

Breaking H said Eta in Two

ανδ Ξοινινγ Τ:Σ:Θ 

ασ Π

ΑΣ Τ

as the

ασ θ

found under the u key

Re~place the word salad image conjured by the letter set: Dielectric

 meaning Motion collector

The state of S~t~asis where 

The thing that is, remains the thing that is

 as is

((=+))

IMAGINARY STASIS SEEMS TO BE IN AIR~TIA

((=+))

as the collection remains collected

in the state of stay home sis

Alternative universes being~:~ 

((+=))

((-=-))

((=--))

((--=))

((++))

(etc)

collections known as Helium where

() = One Electron shell idea

identifying one electric line - idea -

with a size of one electronic ~ ideal ~

are 

move able in the mind as ideas

representing positive direction 

here to fore to be known as the 

Clock Ways 

Clock Wise

CW

and a Counter Clock Way

the Way that can  be named

the way that would change the direction of C

CCW

C squared Waved Uπ

Into The Torque that defines motion in the 

Ψ διρεψτιον

ακα

The C direction

where C is spelled PSI to get the idea across

that bows shoot arrows

where arrows are pointed

The direction in the C idea being 

Circular one C later

Giving C the new new name the Circu~later

For people showing up fashion ably late

Often find twisted into

Helical

The name that later became confused by the Sophist

Later the Sophist ~ ic ate

who were big talkers telling tall tales designed 

to turn this idea into that word by

twisting the word around itself twice 

into tourniquet where 

the Torque used

by the seller of ideas to 

press the coin out of the ignorant

as many times as sequentially possible

using circular logic tricks

leveraged by water weighted sticks 

on the one eared 

language learners of the day

The Four Principles 

are the Four Principal

ideas of/(pH)

as are all

things as

things made of these ideas

Electric Engines:

~:,.~ motion

 be~coming 

By

constantly Coming into ~ wavelength

or S ohm e Amplitude

of~pH some ~ Amplitude 

or Some ~ Wavelength

By C on st anΔ t~ly Going out of 

S Ωημ Sohmhm Amplitude

To Another Amplitude

 and Some Wavelength 

to Another Wavelength

The way Wavelength is used by Color

The way Amplitude is used by Sound

The way Amplitude modulated is Tone

The way every tone is organized using this

Organ

eyes

er

AS: 1. One 360 Degree Circle

 a. cut up 3600 ways

B. at 15 de~G intervals

Cc,. Counted in Motion 

Δ, . Using A or a Ra di e }nt{ ---

e. Magnetic Moment ((x)) Centered Pointer

The blue line is the radical axis of the two tangent circles C₁, C₂ (pink). Each pair of given circles has a homothetic center which belongs to the radical axis of the two tangent circles. Since the radical axis is a line this means that the three homothetic centers are collinear

Phi (/faɪ/;^[1] uppercase Φ, lowercase φ or ϕ; Ancient Greek: ϕεῖ pheî [pʰéî̯]; Modern Greek: φι fi [fi]) is the twenty-first letter of the Greek alphabet.

In Archaic and Classical Greek (c. 9th to 4th century BC), it represented an aspirated voiceless bilabial plosive ([pʰ]), which was the origin of its usual romanization as ⟨ph⟩.

 During the later part of Classical Antiquity, in Koine Greek (c. 4th century BC to 4th century AD), its pronunciation shifted to a voiceless bilabial fricative ([ɸ]), and by the Byzantine Greek period (c. 4th century AD to 15th century AD) it developed its modern pronunciation as a voiceless labiodental fricative ([f]). The romanization of the Modern Greek phoneme is therefore usually ⟨f⟩.

It may be that phi originated as the letter qoppa (Ϙ, ϙ),

 and initially represented the sound /kʷʰ/ 

before shifting to Classical Greek [pʰ].

^[2] In traditional Greek numerals, phi has a value of 500 (φʹ) or 500,000 (͵φ). The Cyrillic letter Ef (Ф, ф) descends from phi.

Pure states of wave functions 

[edit]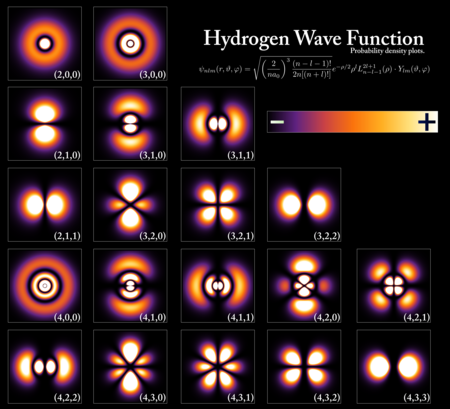

Probability densities for the electron of a hydrogen atom in different quantum states.

 Solutions in quantum mechanics can be expressed as pure States. The  solution states, called eigenstates, are labeled with quantum numbers. 

For example, when dealing with the energy spectrum of the electron in a hydrogen atom, the relevant pure states are identified by the principal quantum number n, 

the angular momentum quantum number ℓ,

 the magnetic quantum number m, 

and the spin z-component s_z. 

For another example, if the spin of an electron is measured in any direction, there are two possible results: up or down.

 A pure state here is represented by a two-dimensional complex vector ${\displaystyle (\alpha ,\beta )}$,

 with a length of one; that is, with$${\displaystyle |\alpha {|}^2+|\beta {|}^2=1,}$$where ${\displaystyle |\alpha |}$ and ${\displaystyle |\beta |}$ are the absolute values of ${\displaystyle \alpha }$ and ${\displaystyle \beta }$.

The postulates of quantum mechanics state that pure states, at a given time t, correspond to vectors in a separable complex Hilbert space, while each measurable physical quantity (such as the energy or momentum of a particle) is associated with a mathematical operator called the observable. The operator serves as a linear function that acts on the states of the system. The eigenvalues of the operator correspond to the possible values of the observable. For example, it is possible to observe a particle with a momentum of 1 kg⋅m/s if and only if one of the eigenvalues of the momentum operator is 1 kg⋅m/s. The corresponding eigenvector (which physicists call an eigenstate) with eigenvalue 1 kg⋅m/s would be a quantum state with a definite, well-defined value of momentum of 1 kg⋅m/s, with no quantum uncertainty. If its momentum were measured, the result is guaranteed to be 1 kg⋅m/s.

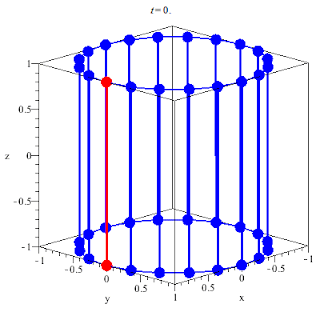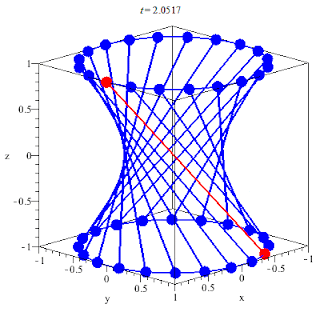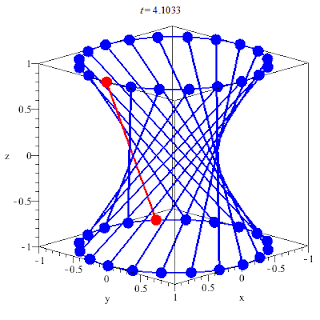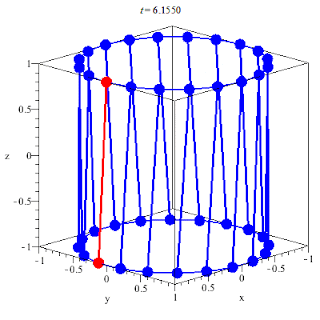
In geometry, a hyperboloid of revolution, 

sometimes called a circular hyperboloid,

 is the surface generated by rotating a hyperbola around one of its principal axes.

 A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry.

Affine transformation

34 languages

• Article
• Talk

• Read
• Edit
• View history

Tools

From Wikipedia, the free encyclopedia

An image of a fern-like fractal (Barnsley's fern) that exhibits affine self-similarity. Each of the leaves of the fern is related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the dark blue leaf and any of the light blue leaves by a combination of reflection, rotation, scaling, and translation.

In Euclidean geometry, an affine transformation or affinity (from the Latin, affinis, "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.

More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.

If X is the point set of an affine space, then every affine transformation on X can be represented as the composition of a linear transformation on X and a translation of X. Unlike a purely linear transformation, an affine transformation need not preserve the origin of the affine space. Thus, every linear transformation is affine, but not every affine transformation is linear.

Examples of affine transformations include translation, scaling, homothety, similarity, reflection, rotation, hyperbolic rotation, shear mapping, and compositions of them in any combination and sequence.

Viewing an affine space as the complement of a hyperplane at infinity of a projective space, the affine transformations are the projective transformations of that projective space that leave the hyperplane at infinity invariant, restricted to the complement of that hyperplane.