Putting the Di in Elec-trick s

Λιφε

Dielectric: When an electric potential difference (a voltage) is applied across the terminals of a capacitor, for example when a capacitor is connected across a battery, an electric field develops across a dielectric, causing a net positive charge to collect on one plate and net negative charge to collect on the other plate. No current actually flows through a perfect dielectric. However, there is a flow of charge through the source circuit.

 When the condition is maintained for a defined number of cycles

the current through the source circuit ceases.

 

Capacitors are widely used as parts of electrical circuits in many common electrical devices. Unlike a resistor, an ideal capacitor does not dissipate energy, although real-life capacitors do dissipate a small amount (see Non-ideal behavior). be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the material as they do in an electrical conductor, because they have no loosely bound, or free, electrons that may drift through the material, but instead they shift, only slightly, from their average equilibrium positions, causing dielectric polarisation. Because of dielectric polarisation, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. This creates an internal electric field that reduces the overall field within the dielectric itself. If a dielectric is composed of weakly bonded molecules, those molecules not only become polarised, but also reorient so that their symmetry axes align to the field.^[1]

The study of dielectric properties concerns storage and dissipation of electric and magnetic energy in materials.^[2][3][4] Dielectrics are important for explaining various phenomena in electronics, optics, solid-state physics and cell biophysics.^[5][6]

A rose is the set of points in polar coordinates specified by the polar equation^[2]

${\displaystyle r=a\cos (k\theta )}$

Each form is formed from the same set of  re~la~ti~on~ships

Petals

[edit]

•  A cycle is a portion of a Sin~us~oid that is one period T = ⁠2π/k⁠ long and consists of a positive half-cycle,
• Graphs of roses are composed of petals. A petal is the shape formed by the graph of a half-cycle of the sinusoid that specifies Θε complete rose.
  
  
  
•  A Ψ~Φ~C~ycle is a portion of a Σinuπσ~oid ωοιδ that is one period T = ⁠2π/k⁠ long and consists of a positive half-cycle, the continuous set of points where r ≥ 0 and is ⁠T/2⁠ = ⁠π/k⁠ long, and a negative half-cycle is the other half where r ≤ 0.)
  • The shape of each petal is same because the graphs of half-cycles have the same shape. The shape is given by the positive half-cycle with crest at (a,0) specified by r = a cos(kθ) (that is bounded by the angle interval −⁠T/4⁠ ≤ θ ≤ ⁠T/4⁠). The petal is symmetric about the polar axis. All other petals are rotations of this petal about the pole, including those for roses specified by the sine function with same values for a and k.^[5]

or in Cartesian coordinates using the parametric equations

A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is simple harmonic motion; as rotation, it corresponds to uniform circular motion. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes.

When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the sine and cosine components, respectively.

Audio example

[edit]

Sine wave

Duration: 5 seconds.0:05

Five seconds of a 220 Hz sine wave. This is the sound wave described by a sine function with f = 220 oscillations per second.

---

Problems playing this file? See media help.

A sine wave represents a single frequency with no harmonics and is considered an acoustically pure tone. Adding sine waves of different frequencies results in a different waveform. Presence of higher harmonics in addition to the fundamental causes variation in the timbre, which is the reason why the same musical pitch played on different instruments sounds different.

Roses can also be specified using the sine function.^[3] Since

${\displaystyle \sin (k\theta )=\cos \left(k\theta -\frac{\pi }{2}\right)=\cos \left(k\left(\theta -\frac{\pi }{2k}\right)\right)}$.

Thus, the rose specified by r = a sin(kθ) is identical to that specified by r = a cos(kθ) rotated counter-clockwise by ⁠π/2k⁠ radians, which is one-quarter the period of either sinusoid.

Since they are specified using the cosine or sine function, roses are usually expressed as polar coordinate (rather than Cartesian coordinate) graphs of sinusoids that have angular frequency of k and an amplitude of a that determine the radial coordinate r given the polar angle θ (though when k is a rational number, a rose curve can be expressed in Cartesian coordinates since those can be specified as algebraic curves^[4]).

As a function of both position and time

[edit]

The displacement of an undamped spring-mass system oscillating around the equilibrium over time is a sine wave.

Sinusoids that exist in both position and time also have:

• a spatial variable ${\displaystyle x}$ that represents the position on the dimension on which the wave propagates.
• a wave number (or angular wave number) ${\displaystyle k}$, which represents the proportionality between the angular frequency ${\displaystyle \omega }$ and the linear speed (speed of propagation) ${\displaystyle v}$:
  • wavenumber is related to the angular frequency by $k=\frac{\omega }{v}=\frac{2\pi f}{v}=\frac{2\pi }{\lambda }$ where ${\displaystyle \lambda }$ (lambda) is the wavelength.

Depending on their direction of travel, they can take the form:

• ${\displaystyle y(x,t)=A\sin (kx-\omega t+\phi )}$, if the wave is moving to the right, or
• ${\displaystyle y(x,t)=A\sin (kx+\omega t+\phi )}$, if the wave is moving to the left.

Since sine waves propagate without changing form in distributed linear systems,^{[definition needed]} they are often used to analyze wave propagation.

 a pure tone is a sound with a sinusoidal waveform; that is, a sine wave of constant frequency, phase-shift, and amplitude.^[1]

 By extension, in signal processing a single-frequency tone or pure tone is a purely sinusoidal signal (e.g., a voltage). A pure tone has the property – unique among real-valued wave shapes – that its wave shape is unchanged by linear time-invariant systems; that is, only the phase and amplitude change between such a system's pure-tone input and its output.

Sine and cosine waves can be used as basic building blocks of more complex waves. As additional sine waves having different frequencies are combined, the waveform transforms from a sinusoidal shape into a more complex shape. When considered as part of a whole spectrum, a pure tone may also be called a spectral component.

In clinical audiology, pure tones are used for pure-tone audiometry to characterize hearing thresholds at different frequencies. Sound localization is often more difficult with pure tones than with other sounds.^[2][3]

Relation to pitch and musical tones

[edit]

Pure tones have been used by 19th century physicists like Georg Ohm and Hermann von Helmholtz to support theories asserting that the ear functions in a way equivalent to a Fourier frequency analysis.^[4][5] In Ohm's acoustic law, later further elaborated by Helmholtz, musical tones are perceived as a set of pure tones. The percept of pitch depends on the frequency of the most prominent tone, and the phases of the individual components is discarded. This theory has often been blamed for creating a confusion between pitch, frequency and pure tones.^[6]

Unlike musical tones that are composed of the sum of a number of harmonically related sinusoidal components, pure tones only contain one such sinusoidal waveform. When presented in isolation, and when its frequency pertains to a certain range, pure tones give rise to a single pitch percept, which can be characterized by its frequency. In this situation, the instantaneous phase of the pure tone varies linearly with time. If a pure tone gives rise to a constant, steady-state percept, then it can be concluded that its phase does not influence this percept. However, when multiple pure tones are presented at once, like in musical tones, their relative phase plays a role in the resulting percept. In such a situation, the perceived pitch is not determined by the frequency of any individual component, but by the frequency relationship between these components (see missing fundamental).

• 
  Pure tone oscillogram of middle C (262 Hz). (Scale: 1 square is equal to 1 millisecond)
 
• 
  Pure tone for C3, an octave below middle C. The frequency is half that of middle C (131 Hz).
 
• 
  Pure tone oscillogram of C5, an octave above middle C. The frequency is twice that of middle C (523 Hz).

Piezoelectricity (/ˌpiːzoʊ-, ˌpiːtsoʊ-, paɪˌiːzoʊ-/, US: /piˌeɪzoʊ-, piˌeɪtsoʊ-/)^[1] is the electric charge that accumulates in certain solid materials—such as crystals, certain ceramics, and biological matter such as bone, DNA, and various proteins—in response to applied mechanical stress.^[2] The word piezoelectricity means electricity resulting from pressure and latent heat. It is derived from Ancient Greek πιέζω (piézō) 'to squeeze or press' and ἤλεκτρον (ḗlektron) 'amber' (an ancient source of static electricity).^[3][4] The German form of the word (Piezoelektricität) was coined in 1881 by the German physicist Wilhelm Gottlieb Hankel; the English word was coined in 1883.^[5][6]

The piezoelectric effect results from the linear electromechanical interaction between the mechanical and electrical states in crystalline materials with no inversion symmetry.^[7] The piezoelectric effect is a reversible process: materials exhibiting the piezoelectric effect also exhibit the reverse piezoelectric effect, the internal generation of a mechanical strain resulting from an applied electric field. For example, lead zirconate titanate crystals will generate measurable piezoelectricity when their static structure is deformed by about 0.1% of the original dimension. Conversely, those same crystals will change about 0.1% of their static dimension when an external electric field is applied. The inverse piezoelectric effect is used in the production of ultrasound waves.^[8]

Quartz is one member of a family of crystals that experience the piezoelectric effect. The piezoelectric effect has found applications in high power sources, sensors, actuators, frequency standards, motors, etc., and the relationship between applied voltage and mechanical deformation is well known; this allows probing an acoustic resonance by electrical means. Applying alternating current to the quartz crystal will induce oscillations. With an alternating current between the electrodes of a properly cut crystal, a standing shear wave is generated. The Q factor, which is the ratio of frequency and bandwidth, can be as high as 10⁶. Such a narrow resonance leads to highly stable oscillators and a high accuracy in the determination of the resonance frequency. The QCM exploits this ease and precision for sensing. Common equipment allows resolution down to 1 Hz on crystals with a fundamental resonant frequency in the 4 – 6 MHz range. A typical setup for the QCM contains water cooling tubes, the retaining unit, frequency sensing equipment through a microdot feed-through, an oscillation source, and a measurement and recording device.

The frequency of oscillation of the quartz crystal is partially dependent on the thickness of the crystal. During normal operation, all the other influencing variables remain constant; thus a change in thickness correlates directly to a change in frequency. As mass is deposited on the surface of the crystal, the thickness increases; consequently the frequency of oscillation decreases from the initial value. With some simplifying assumptions, this frequency change can be quantified and correlated precisely to the mass change using the Sauerbrey equation.^[2] Other techniques for measuring the properties of thin films include ellipsometry, surface plasmon resonance (SPR) spectroscopy, Multi-Parametric Surface Plasmon Resonance and dual polarisation interferometry.

Quartz is a hard, crystalline mineral composed of silica (silicon dioxide). The atoms are linked in a continuous framework of SiO₄ silicon–oxygen tetrahedra, with each oxygen being shared between two tetrahedra, giving an overall chemical formula of SiO₂. Quartz is, therefore, classified structurally as a framework silicate mineral and compositionally as an oxide mineral. Quartz is the second most abundant mineral in Earth's continental crust, behind feldspar.^[10]

Quartz exists in two forms, the normal α-quartz and the high-temperature β-quartz, both of which are chiral. The transformation from α-quartz to β-quartz takes place abruptly at 573 °C (846 K; 1,063 °F). Since the transformation is accompanied by a significant change in volume, it can easily induce microfracturing of ceramics or rocks passing through this temperature threshold.

The oxide mineral class includes those minerals in which the oxide anion (O²⁻) is bonded to one or more metal alloys. The hydroxide-bearing minerals are typically included in the oxide class. Minerals with complex anion groups such as the silicates, sulfates, carbonates and phosphates are classed separately.

An ion (/ˈaɪ.ɒn, -ən/)^[1] is an atom or molecule with a net electrical charge. The charge of an electron is considered to be negative by convention and this charge is equal and opposite to the charge of a proton, which is considered to be positive by convention. The net charge of an ion is not zero because its total number of electrons is unequal to its total number of protons.

A cation is a positively charged ion with fewer electrons than protons^[2] (e.g. K⁺ (potassium ion)) while an anion is a negatively charged ion with more electrons than protons.^[3] (e.g. Cl⁻ (chloride ion) and OH⁻ (hydroxide ion)). Opposite electric charges are pulled towards one another by electrostatic force, so cations and anions attract each other and readily form ionic compounds.

If only a + or - is present, it indicates a +1 or -1 charge. To indicate a more severe charge, the number of additional or missing electrons is supplied, as seen in O₂^2- (negative charge, peroxide) and He²⁺ (positive charge, alpha particle).^[4]

Ions consisting of only a single atom are termed atomic or monatomic ions, while two or more atoms form molecular ions or polyatomic ions. In the case of physical ionization in a fluid (gas or liquid), "ion pairs" are created by spontaneous molecule collisions, where each generated pair consists of a free electron and a positive ion.^[5] Ions are also created by chemical interactions, such as the dissolution of a salt in liquids, or by other means, such as passing a direct current through a conducting solution, dissolving an anode via ionization.

In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems (hexagonal and trigonal) and two lattice systems (hexagonal and rhombohedral). While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent (see section crystal systems below).^[1] In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice (such as α-quartz).

The hexagonal crystal family consists of the 12 point groups such that at least one of their space groups has the hexagonal lattice as underlying lattice, and is the union of the hexagonal crystal system and the trigonal crystal system.^[2] There are 52 space groups associated with it, which are exactly those whose Bravais lattice is either hexagonal or rhombohedral

Crystal system	Trigonal		Hexagonal
Lattice system	Rhombohedral	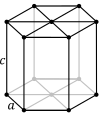Hexagonal
Example	Dolomite (white)	α-Quartz	Beryl

Crystal systems

[edit]

Crystal system	Required symmetries of point group	Point groups	Space groups	Bravais lattices	Lattice system
Trigonal	1 threefold axis of rotation	5	7	1	Rhombohedral
			18	1	Hexagonal
Hexagonal	1 sixfold axis of rotation	7	27

The hexagonal crystal family consists of two crystal systems: trigonal and hexagonal. A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system (see table in Crystal system#Crystal classes).

The trigonal crystal system consists of the 5 point groups that have a single three-fold rotation axis, which includes space groups 143 to 167. These 5 point groups have 7 corresponding space groups (denoted by R) assigned to the rhombohedral lattice system and 18 corresponding space groups (denoted by P) assigned to the hexagonal lattice system. Hence, the trigonal crystal system is the only crystal system whose point groups have more than one lattice system associated with their space groups.

The hexagonal crystal system consists of the 7 point groups that have a single six-fold rotation axis. These 7 point groups have 27 space groups (168 to 194), all of which are assigned to the hexagonal lattice system.