Hypotrochoid with a deeply caring vengence for recycling

Hippocrates Lune Proof

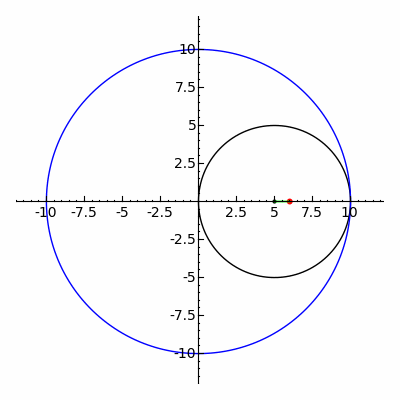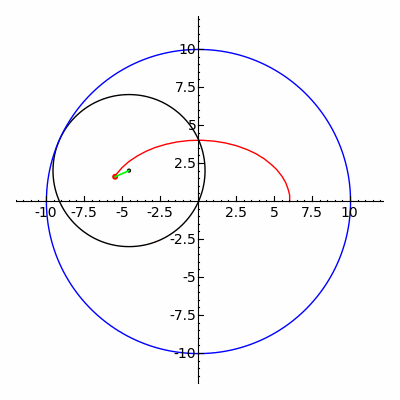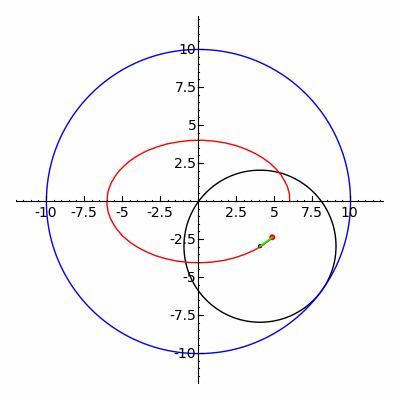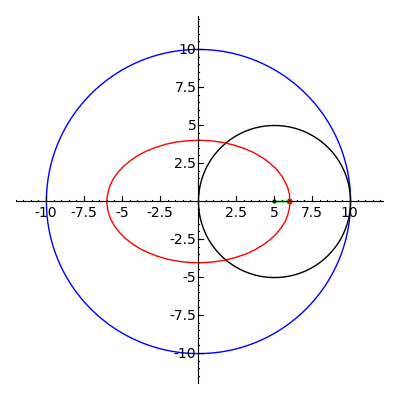
Let the Lune be De fined

By Arc AEB~f

De fined by the Circle 

Centered at Point D

And A Chord of

Circle ABC De Fined

By Center point O

The Area of the Lune is

Found outside

Circle ABC

AND

 equal to

The Area of Isocoles Triangle

ABO

Found Inside Circle ABC

Proof

[edit]

Hippocrates' result can be written as follows: 

The point D is 

The center of The Circle on Which 

The arc AEB lies,

The point D is 

the midpoint of the hypotenuse of

 the isosceles right triangle ABO. 

The length of Line AB is 

Given by the only formula in Mathematics

[AB squared] [is equal to] [AO squared added to OB Squared]

And

For an Isosceles Triangle Δεφινεδ 

ασ a Tri angled pHorm pHormed pHrom two sides 

Joined by 

One Right Angle

Therefore

 The diameter AC

 of the larger circle ABC is ⁠${\displaystyle \sqrt{2}}$⁠ 

times the diameter of the smaller circle

Which is ⁠

Making AC equal to ⁠⁠  Χ ⁠ 

or TWO⁠⁠⁠

 Where the arc AEB  is found

Therefore, 

the smaller circle has 

half the area of the larger circle,

 Therefore

 the quarter circle AFBOA

 is equal in area to the semicircle AEBDA.

 The crescent-shaped area AFBDA 

IS part of Both PArts

and so when Added to

the quarter circle gives triangle ABO 

and Adding the same crescent 

to the semicircle gives the lune. 

Since the triangle and lune are 

both formed by 

Adding

an equal area 

from equal areas, 

To Equal areas

the Sum of the areas themselves 

ARE equal in area.^[2][6]

Interesting claim

If the image was different from

the image of an Owl

the Ma

used

for more than 5000 years

as an idea

it

might

be

worth

its weight in salt

In chemistry, a zwitterion (/ˈtsvɪtəˌraɪən/ TSVIT-ə-ry-ən; 

from German Zwitter [ˈtsvɪtɐ] 'hermaphrodite'), 

also called an inner salt or dipolar ion,^[1] 

is a molecule that contains an equal number of positively and negatively charged functional groups.^[2] 

1,2-dipolar compounds, such as ylides, are sometimes excluded from the definition.^[3]

Applying Ampère's circuital law to the solenoid (see figure on the left) gives us

${\displaystyle Bl={\mu }_{0}NI,}$

where ${\displaystyle B}$ is the magnetic flux density, ${\displaystyle l}$ is the length of the solenoid, ${\displaystyle {\mu }_0}$ is the magnetic constant, ${\displaystyle N}$ the number of turns, and ${\displaystyle I}$ the current. From this we get

${\displaystyle B={\mu }_0\frac{NI}{l}.}$

This equation is valid for a solenoid in free space, which means the permeability of the magnetic path is the same as permeability of free space, μ₀.

If the solenoid is immersed in a material with relative permeability μ_r, then the field is increased by that amount:

${\displaystyle B={\mu }_0{\mu }_{\mathrm{r}}\frac{NI}{l}.}$

The vacuum magnetic permeability (variously vacuum permeability, permeability of free space, permeability of vacuum, magnetic constant) is the magnetic permeability in a classical vacuum. It is a physical constant, conventionally written as μ₀ (pronounced "mu nought" or "mu zero"). It quantifies the strength of the magnetic field induced by an electric current. Expressed in terms of SI base units, it has the unit kg⋅m⋅s⁻²⋅A⁻². It can be also expressed in terms of SI derived units, N⋅A⁻².

Since the revision of the SI in 2019 (when the values of e and h were fixed as defined quantities), μ₀ is an experimentally determined constant, its value being proportional to the dimensionless fine-structure constant, which is known to a relative uncertainty of 1.6×10⁻¹⁰,^[1][2][3][4] with no other dependencies with experimental uncertainty. Its value in SI units as recommended by CODATA is:

μ₀ = 1.25663706127(20)×10⁻⁶ N⋅A^−2[5]

The terminology of permeability and susceptibility was introduced by William Thomson, 1st Baron Kelvin in 1872.^[6] The modern notation of permeability as μ and permittivity as ε has been in use since the 1950s.

The Breadth ορΗ βγεαΔ Θ

As the Motion of

Ba~re~a~th